∫ (x² + 4x³ + 2) / (6x) dx
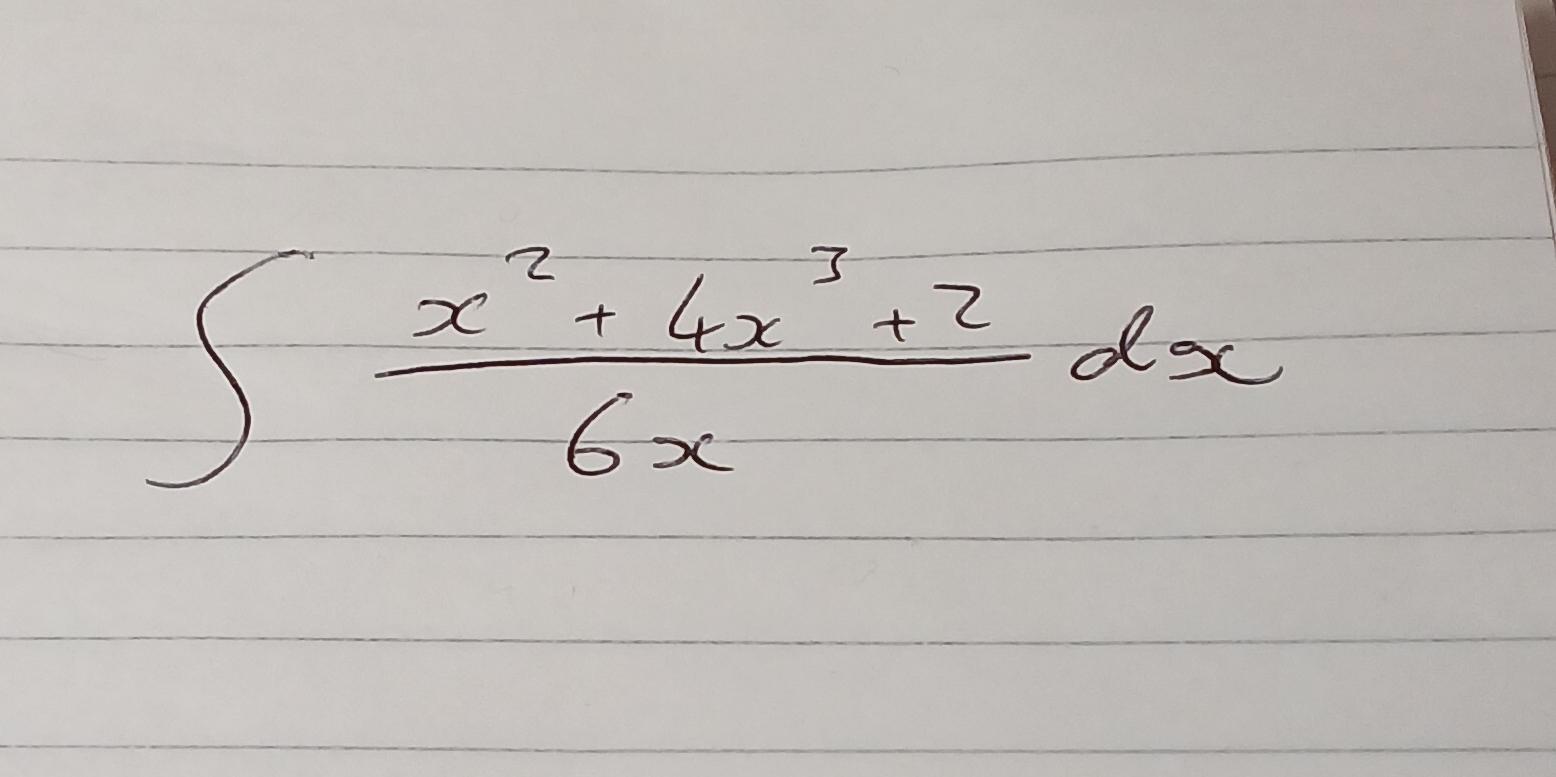
Understand the Problem
The question is asking us to solve the integral of a rational function represented by a fraction involving polynomials. We need to simplify and integrate the expression accordingly.
Answer
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Answer for screen readers
The final answer is:
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Steps to Solve
- Simplify the Expression
First, divide each term in the numerator by the denominator:
$$ \frac{x^2}{6x} + \frac{4x^3}{6x} + \frac{2}{6x} $$
This simplifies to:
$$ \frac{x}{6} + \frac{2x^2}{3} + \frac{1}{3x} $$
- Set Up the Integral
Now, set up the integral with the simplified expression:
$$ \int \left( \frac{x}{6} + \frac{2x^2}{3} + \frac{1}{3x} \right) dx $$
- Integrate Each Term
Integrate each term separately:
- For $\frac{x}{6}$:
$$ \int \frac{x}{6} dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} $$
- For $\frac{2x^2}{3}$:
$$ \int \frac{2x^2}{3} dx = \frac{2}{3} \cdot \frac{x^3}{3} = \frac{2x^3}{9} $$
- For $\frac{1}{3x}$:
$$ \int \frac{1}{3x} dx = \frac{1}{3} \ln |x| $$
- Combine the Results
Combine all the integrals together:
$$ \int \left( \frac{x}{6} + \frac{2x^2}{3} + \frac{1}{3x} \right) dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
where $C$ is the constant of integration.
The final answer is:
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
More Information
This integral involves basic polynomial integration and the natural logarithm of a linear term. The process showcases how to simplify a rational function before integration, making it easier to manage.
Tips
- Forgetting the integration constant: Always remember to add the constant of integration ( C ).
- Improper simplification: Ensure that each term is simplified correctly before integration.