∫ (x² + 4x + 2) / (6x) dx
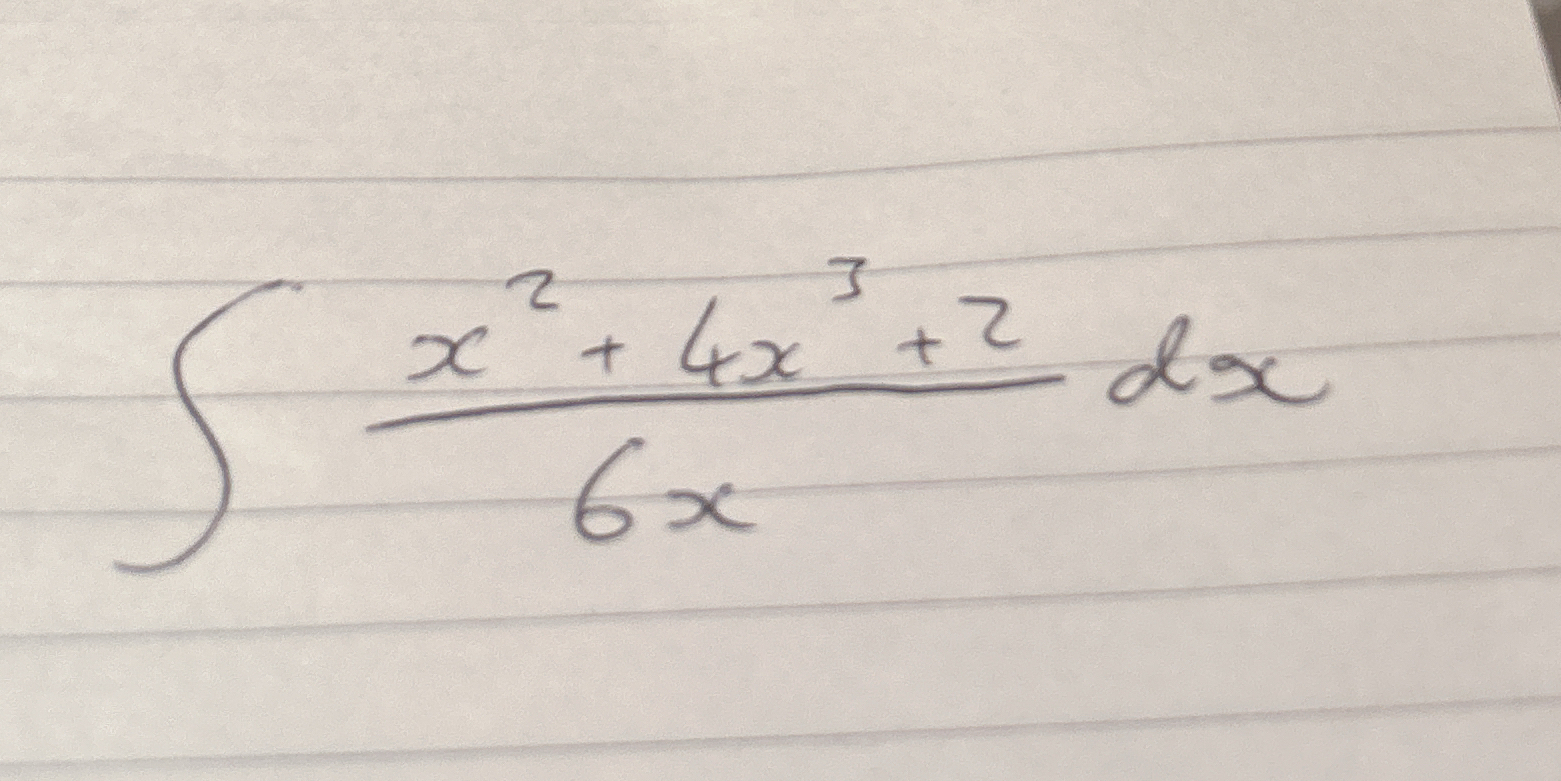
Understand the Problem
The question is asking to evaluate the integral of the expression (x² + 4x + 2) / (6x) with respect to x. This involves simplifying the integrand and then finding its antiderivative.
Answer
The integral evaluates to $$ \frac{x^2}{12} + \frac{2}{3} x + \frac{1}{3} \ln |x| + C $$
Answer for screen readers
The evaluated integral is
$$ \frac{x^2}{12} + \frac{2}{3} x + \frac{1}{3} \ln |x| + C $$
Steps to Solve
- Simplify the integrand
We start with the integral
$$ \int \frac{x^{2} + 4x + 2}{6x} , dx $$
To simplify, divide each term in the numerator by (6x):
$$ \int \left( \frac{x^2}{6x} + \frac{4x}{6x} + \frac{2}{6x} \right) dx $$
This simplifies to:
$$ \int \left( \frac{x}{6} + \frac{2}{3} + \frac{1}{3x} \right) dx $$
- Integrate each term separately
Now we can integrate each term:
$$ \int \left( \frac{x}{6} \right) dx + \int \left( \frac{2}{3} \right) dx + \int \left( \frac{1}{3x} \right) dx $$
The integrals are calculated as follows:
- For ( \frac{x}{6} ):
$$ \int \frac{x}{6} , dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} $$
- For ( \frac{2}{3} ):
$$ \int \frac{2}{3} , dx = \frac{2}{3} x $$
- For ( \frac{1}{3x} ):
$$ \int \frac{1}{3x} , dx = \frac{1}{3} \ln |x| $$
- Combine the results
Now, we combine all the results:
$$ \frac{x^2}{12} + \frac{2}{3} x + \frac{1}{3} \ln |x| + C $$
Where (C) is the constant of integration.
The evaluated integral is
$$ \frac{x^2}{12} + \frac{2}{3} x + \frac{1}{3} \ln |x| + C $$
More Information
This problem involves basic algebraic manipulation and the fundamental theorem of calculus. The logarithmic term arises from integrating the function (\frac{1}{x}), a common occurrence in integral calculus.
Tips
- Forgetting the constant of integration: Always include the constant (C) when evaluating indefinite integrals.
- Incorrectly simplifying the integrand: Make sure each term is correctly divided by the common denominator.