∫ (x^2 + 4x + 2) / (6x) dx

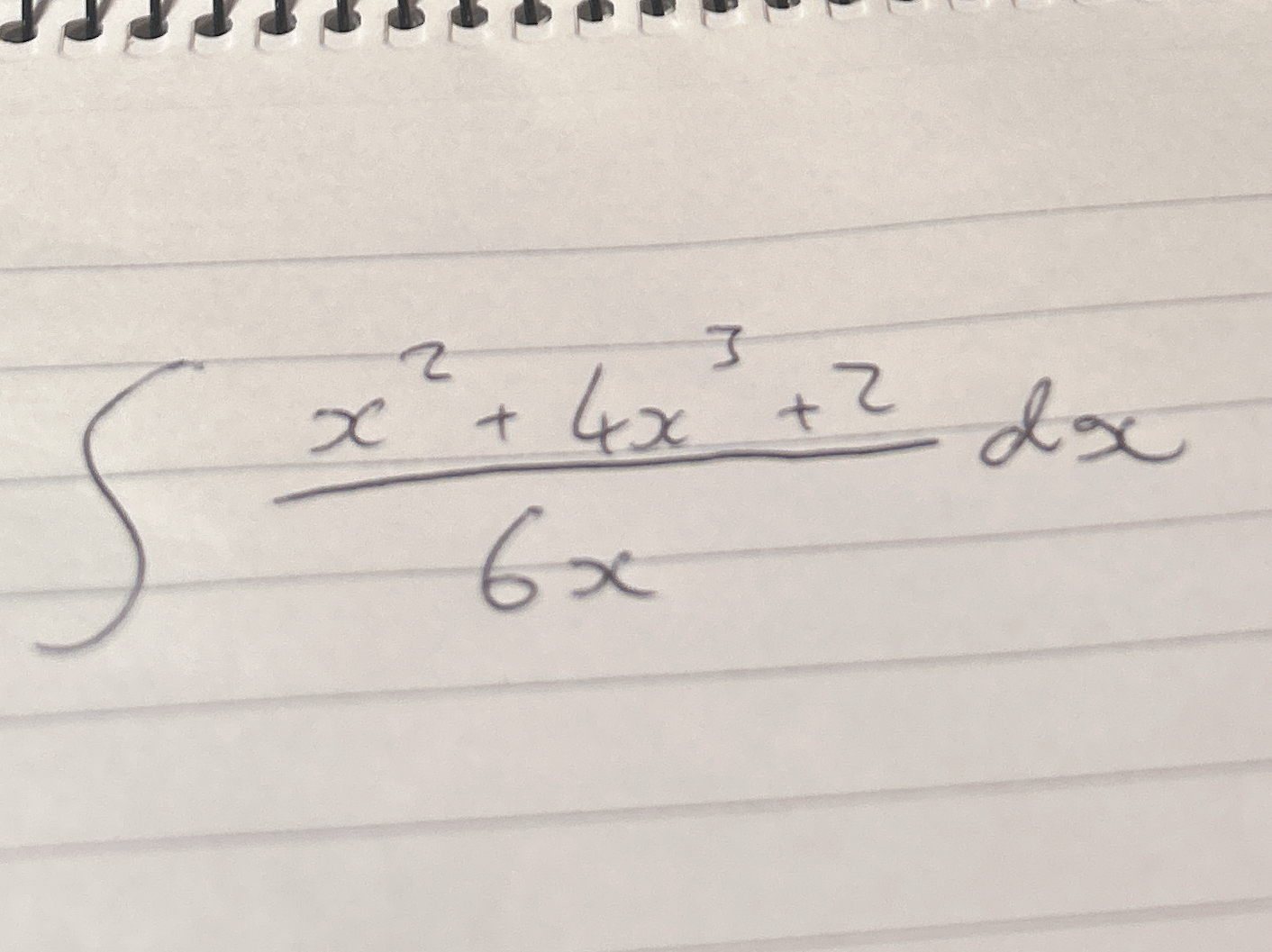
Understand the Problem

The question is asking for the integral of the rational function (x^2 + 4x + 2) / (6x) with respect to x. This entails applying techniques of integration, likely involving simplifying the expression and integrating term by term.

Answer

$$ \int \frac{x^2 + 4x + 2}{6x} \, dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{1}{3} \ln |x| + C $$

Steps to Solve

Simplify the integrand

First, we simplify the expression inside the integral. We can rewrite the rational function:

$$ \frac{x^2 + 4x + 2}{6x} = \frac{x^2}{6x} + \frac{4x}{6x} + \frac{2}{6x} $$

This simplifies to:

$$ \frac{x}{6} + \frac{2}{3} + \frac{1}{3x} $$

Set up the integral

Now we rewrite the integral with the simplified expression:

$$ \int \left( \frac{x}{6} + \frac{2}{3} + \frac{1}{3x} \right) dx $$

Integrate term by term

We integrate each term separately:

For the first term, $\int \frac{x}{6} , dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12}$
For the second term, $\int \frac{2}{3} , dx = \frac{2}{3} x$
For the third term, $\int \frac{1}{3x} , dx = \frac{1}{3} \ln |x|$

Combining these results gives:

$$ \frac{x^2}{12} + \frac{2}{3} x + \frac{1}{3} \ln |x| + C $$

where (C) is the constant of integration.

The integral is

$$ \int \frac{x^2 + 4x + 2}{6x} , dx = \frac{x^2}{12} + \frac{2}{3} x + \frac{1}{3} \ln |x| + C $$

More Information

This integral combines polynomial and logarithmic integration techniques. Each term in the simplified integrand allows for straightforward integration, culminating in a mix of polynomial and logarithmic results.

Tips

Forgetting to apply the linearity of integrals: Some may try to combine terms incorrectly instead of integrating them separately. Always break it into simpler integrable parts.
Misapplying logarithm properties: When dealing with fractions that involve logarithms, ensure correct application of the absolute function.

Thank you for voting!