(x-2)(x^2 + 8x - 1) - (x+4)(x^2 - 5x + 9)

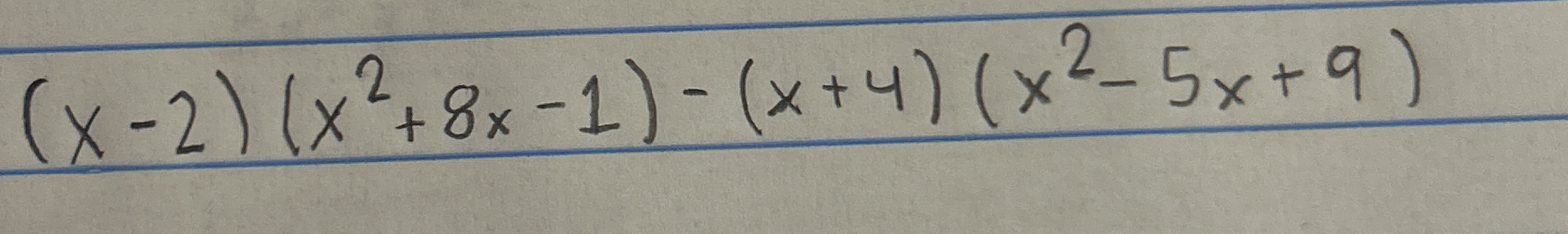
Understand the Problem

The question is presenting a mathematical expression involving polynomials that requires simplification or expansion. The goal is to apply algebraic rules to solve the expression correctly.

Answer

The simplified expression is $ 7x^2 - 6x - 34 $.

Steps to Solve

Expand the first polynomial expression

We start with the expression $(x-2)(x^2 + 8x - 1)$. We will use the distributive property (also known as the FOIL method for binomials).

[ \begin{align*} (x - 2)(x^2 + 8x - 1) &= x(x^2 + 8x - 1) - 2(x^2 + 8x - 1) \ &= x^3 + 8x^2 - x - 2x^2 - 16x + 2 \ &= x^3 + (8x^2 - 2x^2) + (-x - 16x) + 2 \ &= x^3 + 6x^2 - 17x + 2. \end{align*} ]

Expand the second polynomial expression

Next, we expand the expression $(x+4)(x^2 - 5x + 9)$ using the distributive property.

[ \begin{align*} (x + 4)(x^2 - 5x + 9) &= x(x^2 - 5x + 9) + 4(x^2 - 5x + 9) \ &= x^3 - 5x^2 + 9x + 4x^2 - 20x + 36 \ &= x^3 + (-5x^2 + 4x^2) + (9x - 20x) + 36 \ &= x^3 - x^2 - 11x + 36. \end{align*} ]

Combine both expanded expressions

Now we will substitute the expanded forms back into the original question:

[ (x^3 + 6x^2 - 17x + 2) - (x^3 - x^2 - 11x + 36). ]

Simplify the expression

Distribute the negative sign and combine like terms:

[ \begin{align*} &= x^3 + 6x^2 - 17x + 2 - x^3 + x^2 + 11x - 36 \ &= (x^3 - x^3) + (6x^2 + x^2) + (-17x + 11x) + (2 - 36) \ &= 0 + 7x^2 - 6x - 34 \ &= 7x^2 - 6x - 34. \end{align*} ]

The simplified expression is ( 7x^2 - 6x - 34 ).

More Information

The expression represents a quadratic polynomial in standard form. Quadratic polynomials can have different types of roots, and the solutions may be found using the quadratic formula if needed.

Tips

Forgetting to distribute the negative sign when subtracting the second expanded polynomial can lead to incorrect results.
Miscombining like terms, especially with positive and negative coefficients.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!