∫ (x - 1)e^(x^2) / e^(2x) dx
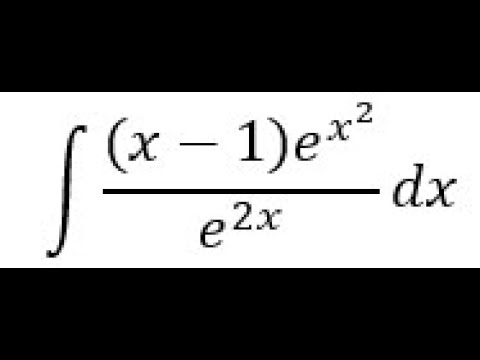
Understand the Problem
The question is asking to evaluate the integral of the expression given, which involves the functions (x - 1)e^(x^2) and e^(2x). The approach will involve applying integration techniques, likely including substitution or parts.
Answer
$$ \frac{1}{2} e^{x^2 - 2x} + C $$
Answer for screen readers
The final evaluated integral is
$$ \frac{1}{2} e^{x^2 - 2x} + C $$
Steps to Solve
- Rewrite the Integral
First, rewrite the integral to simplify the expression inside. We have:
$$ \int \frac{(x - 1)e^{x^2}}{e^{2x}} dx = \int (x - 1)e^{x^2 - 2x} dx $$
- Substitute for Simplification
Make the substitution ( u = x^2 - 2x ). Then, we differentiate ( u ):
$$ \frac{du}{dx} = 2x - 2 \implies du = (2x - 2) dx $$
Rearranging gives us:
$$ dx = \frac{du}{2(x - 1)} $$
- Change the Variables in the Integral
Now substitute ( u ) and ( dx ) into the integral:
$$ \int (x - 1)e^{u} \frac{du}{2(x - 1)} = \frac{1}{2} \int e^u du $$
- Integrate the Function
The integral of ( e^u ) is:
$$ \int e^u du = e^u + C $$
Hence,
$$ \frac{1}{2} \int e^u du = \frac{1}{2} e^u + C $$
- Back Substitute to Original Variable
Finally, substitute back in for ( u ):
$$ \frac{1}{2} e^{x^2 - 2x} + C $$
The final evaluated integral is
$$ \frac{1}{2} e^{x^2 - 2x} + C $$
More Information
This result reflects how integration techniques such as substitution can simplify complex integrals, particularly when exponential functions are involved. The original function can often be transformed to a more manageable form, allowing easier integration.
Tips
- Forgetting to change the limits of integration if definite.
- Leaving out the constant of integration ( C ).
- Confusing where to place the ( dx ) (make sure to substitute correctly).
AI-generated content may contain errors. Please verify critical information