Write the equation of the line graphed below in simplest form.
Understand the Problem
The question is asking for the equation of a line based on the graph provided. To solve it, we need to identify the slope and the y-intercept from the graph to formulate the equation in slope-intercept form (y = mx + b).
Answer
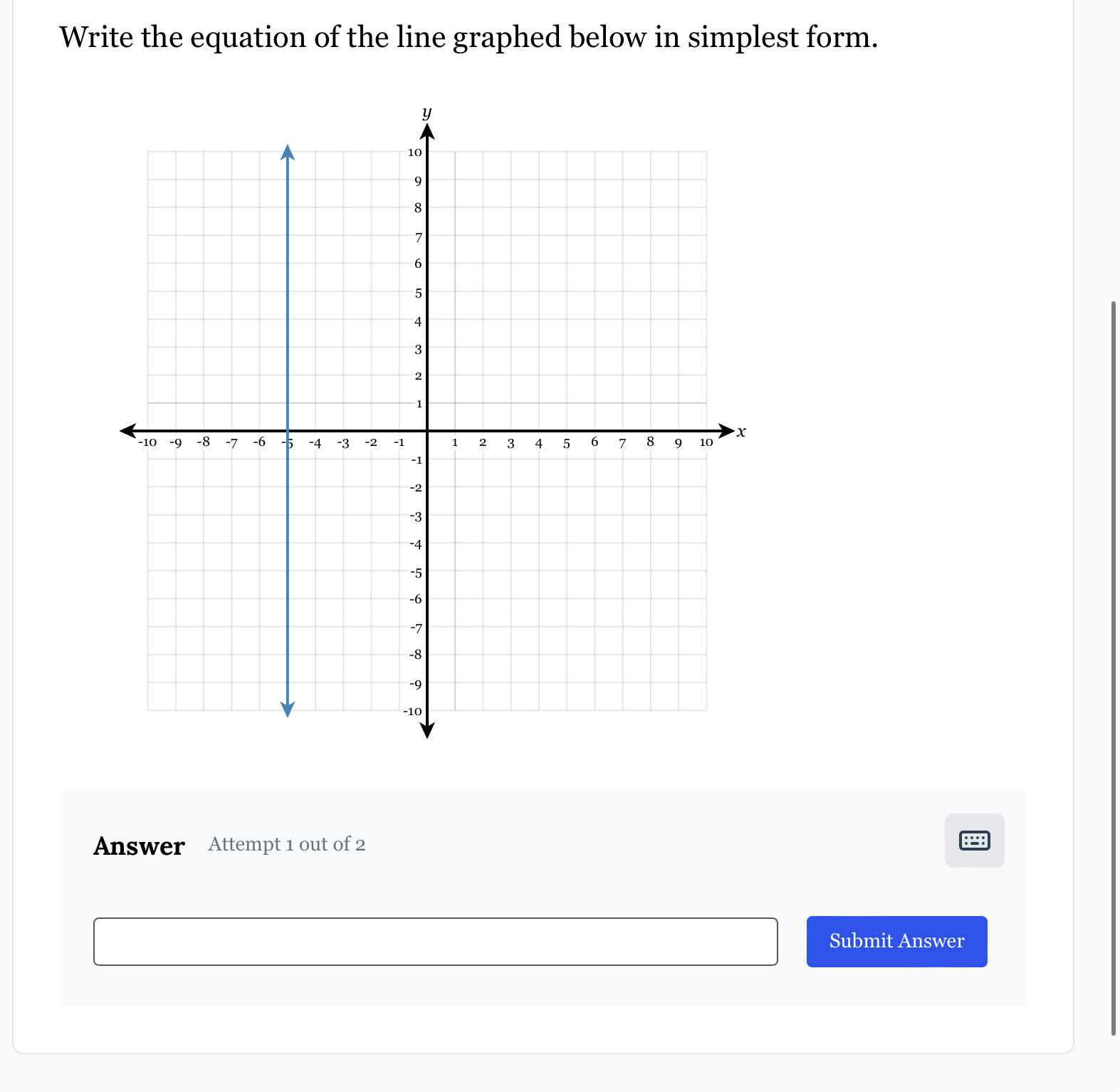
The equation of the line is \(x = -5\).
Answer for screen readers
The equation of the line in simplest form is (x = -5).
Steps to Solve
- Identify the Slope (m)
From the graph, determine two points on the line. For example, let’s say the line passes through points ((-5, -10)) and ((-5, 0)). The change in (y) (rise) is (10) (from (-10) to (0)) and the change in (x) (run) is (0) (since the x-coordinate doesn’t change).
The slope (m) can be calculated as: $$ m = \frac{\text{rise}}{\text{run}} = \frac{10}{0} $$ This indicates that the slope is undefined, which means the line is vertical.
- Identify the Y-Intercept (b)
For a vertical line, the (y)-intercept is not defined since it does not cross the y-axis; however, the equation of a vertical line is given by (x = k), where (k) is the x-coordinate of any point on the line.
In our example, since the line passes through ((-5, y)), we have: $$ x = -5 $$
- Write the Equation of the Line
Since we have established that the line is vertical, the final equation of the line is: $$ x = -5 $$
The equation of the line in simplest form is (x = -5).
More Information
Vertical lines have equations in the form of (x = k), where (k) represents the x-coordinate where the line is located. This type of line does not have a slope in the traditional sense, as it runs parallel to the y-axis.
Tips
- Confusing vertical lines with horizontal lines, which have the form (y = k) and involve slope calculations.
- Not recognizing that a vertical line does not have a defined slope.
