Write the demand function (equation) showing the relationship between the quantity of vaccine demanded (Q) and the price (P). Using the data above.
Understand the Problem
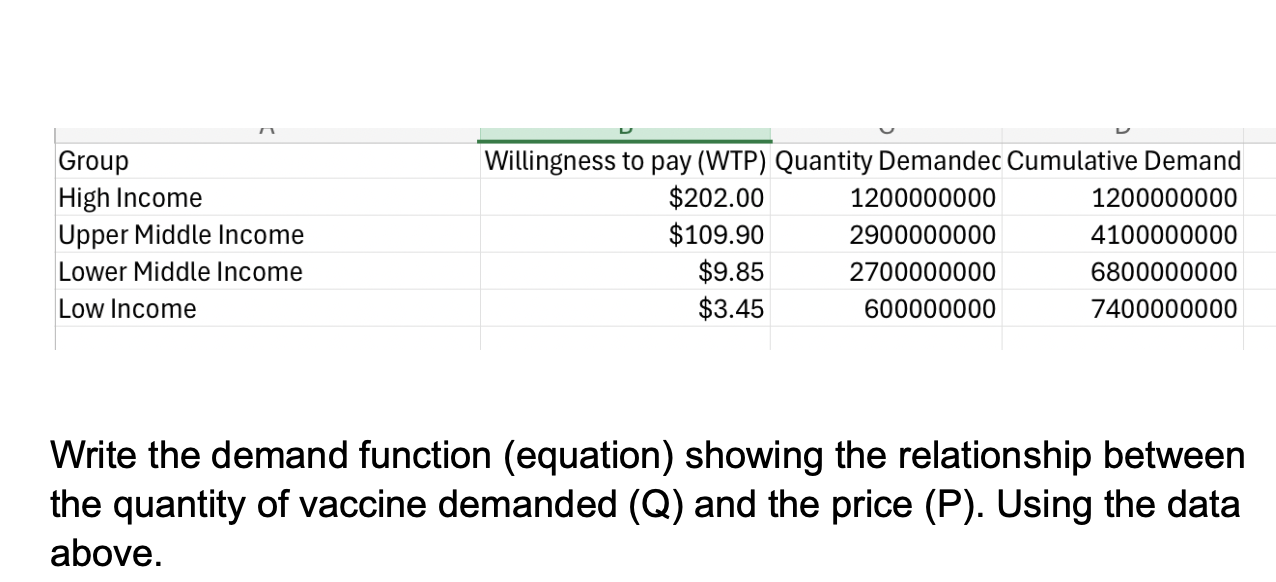
The question asks for a demand function that relates the quantity of vaccine demanded (Q) to the price (P), based on the willingness to pay (WTP) and quantity demanded provided in the image. To solve this, we need to analyze the given data to derive the equation that represents this relationship.
Answer
The demand function is given by: $$ Q = -2,414,730.754P + 607,487,557.5 $$
Answer for screen readers
The demand function is given by: $$ Q = -2,414,730.754P + 607,487,557.5 $$
Steps to Solve
- Extract Data We have the following willingness to pay (WTP) and quantity demanded (Q) from the table:
- WTP: $202.00, Q: 120,000,000 (High Income)
- WTP: $109.90, Q: 290,000,000 (Upper Middle Income)
- WTP: $9.85, Q: 270,000,000 (Lower Middle Income)
- WTP: $3.45, Q: 600,000,000 (Low Income)
- Create Points Using the WTP and quantity demanded, we create points in the form $(P, Q)$:
- $(202, 120,000,000)$
- $(109.9, 290,000,000)$
- $(9.85, 270,000,000)$
- $(3.45, 600,000,000)$
- Determine Demand Function We can derive the linear equation connecting price and quantity. Generally, we use two points to find the slope ( m ): Using the points $(202, 120,000,000)$ and $(3.45, 600,000,000)$:
The slope $m$ is calculated as: $$ m = \frac{Q_2 - Q_1}{P_2 - P_1} = \frac{600,000,000 - 120,000,000}{3.45 - 202} = \frac{480,000,000}{-198.55} $$
-
Linear Equation Format The linear equation is formulated as: $$ Q = mP + b $$ Where ( b ) can be determined using one of the points.
-
Calculate Slope Calculating the slope using the formula from Step 3: $$ m \approx -2,414,730.754 $$
-
Find Intercept (b) Using one point to find ( b ). Using the point $(202, 120,000,000)$:
$$ 120,000,000 = -2,414,730.754(202) + b $$
Rearranging gives us: $$ b = 120,000,000 + 487,487,557.5 $$
Calculating ( b ): $$ b \approx 607,487,557.5 $$
- Final Demand Equation Substituting ( m ) and ( b ) back into the equation: $$ Q = -2,414,730.754P + 607,487,557.5 $$
The demand function is given by: $$ Q = -2,414,730.754P + 607,487,557.5 $$
More Information
The demand function describes how the quantity of vaccines demanded decreases as the price increases. Each additional dollar in price can significantly lower the quantity demanded by a large number of units, reflecting the sensitivity of demand to price changes.
Tips
- Incorrectly calculating slope: Ensure to correctly subtract quantity and price values.
- Confusing ( P ) and ( Q ): Remember that ( P ) is the price and ( Q ) is the quantity.
AI-generated content may contain errors. Please verify critical information