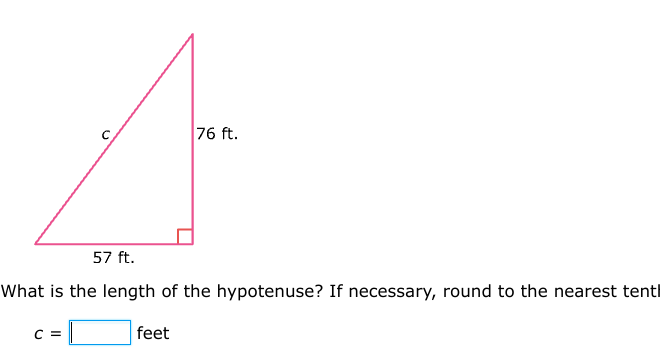
What is the length of the hypotenuse? If necessary, round to the nearest tenth.
Understand the Problem
The question is asking for the length of the hypotenuse in a right triangle where one side is 76 feet and the other side is 57 feet. We will use the Pythagorean theorem (a² + b² = c²) to find it.
Answer
The length of the hypotenuse is $c = 95$ feet.
Answer for screen readers
The length of the hypotenuse is $c = 95$ feet.
Steps to Solve
-
Identify the sides In this right triangle, the lengths of the sides are given: one side ($a$) is 76 feet and the other side ($b$) is 57 feet.
-
Apply the Pythagorean theorem According to the Pythagorean theorem, the formula to find the hypotenuse ($c$) is: $$ c = \sqrt{a^2 + b^2} $$
-
Calculate the squares of the sides First, find the squares of each side:
- $a^2 = 76^2 = 5776$
- $b^2 = 57^2 = 3249$
-
Find the sum of the squares Now, add the squares of the two sides: $$ a^2 + b^2 = 5776 + 3249 = 9025 $$
-
Calculate the hypotenuse Finally, take the square root to find the hypotenuse: $$ c = \sqrt{9025} $$
-
Round if necessary Calculating this gives $c = 95$ feet. Since it's already a whole number, no rounding is needed.
The length of the hypotenuse is $c = 95$ feet.
More Information
The Pythagorean theorem is a fundamental principle in geometry that relates the lengths of the sides of a right triangle. It states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Tips
- Forgetting to square the lengths of the sides before adding them.
- Confusing the placement of the sides in the Pythagorean theorem.
AI-generated content may contain errors. Please verify critical information