Write the demand function (equation) showing the relationship between the quantity of vaccine demanded (Q) and the price (P). Using the data above.
Understand the Problem
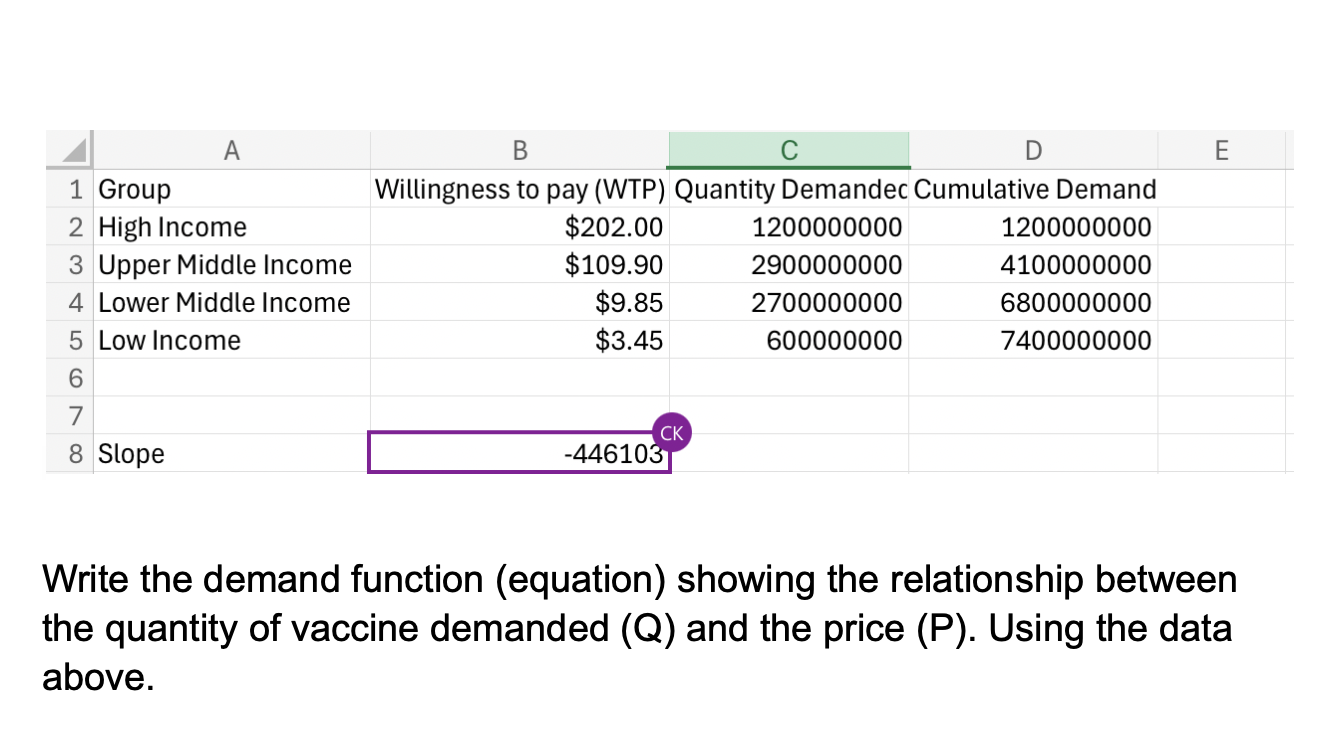
The question is asking to derive a demand function that relates the quantity of vaccine demanded (Q) to the price (P) based on the provided data. This involves using the slope provided and the values of price and quantity demanded from the table to formulate the equation.
Answer
The demand function is $Q = -446103P + 12090160106$.
Answer for screen readers
The demand function is given by:
$$ Q = -446103P + 12090160106 $$
Steps to Solve
- Identify Known Values
From the data provided, we have the following prices (willingness to pay) and the corresponding quantities demanded:
- Price (P) values: $202, $109.90, $9.85, $3.45$
- Quantity (Q) values: $12000000000, 29000000000, 27000000000, 6000000000$
- Calculate Average Slope
The slope is provided as $-446103$. This slope will be used in the demand function.
- Select a Point
Choose a point from the data set to serve as the point to compute the intercept. Let's use the first point:
- Price $P = 202$ and Quantity $Q = 12000000000$.
- Use Point-Slope Form to Find the Demand Function
We can use the point-slope equation:
$$ Q - Q_0 = m(P - P_0) $$
Where:
- ( m = -446103 )
- ( Q_0 = 12000000000 )
- ( P_0 = 202 )
- Rearranging to Find the Demand Function
Substituting the known values into the equation:
$$ Q - 12000000000 = -446103(P - 202) $$
This can be rearranged to find ( Q ):
$$ Q = -446103P + 446103 \cdot 202 + 12000000000 $$
- Calculate the Intercept
Now calculate ( 446103 \cdot 202 ):
$$ 446103 \cdot 202 = 90160106 $$
Thus, the equation becomes:
$$ Q = -446103P + 90160106 + 12000000000 $$
Combine the constant terms:
$$ Q = -446103P + 12090160106 $$
The demand function is given by:
$$ Q = -446103P + 12090160106 $$
More Information
This demand function indicates how the quantity of vaccine demanded ($Q$) decreases as the price ($P$) increases. The negative slope reflects the inverse relationship typical of demand curves—when the price goes up, the quantity demanded generally goes down.
Tips
- Misinterpreting the slope as a positive value when it is negative.
- Forgetting to use the correct point from the data while calculating the intercept.
- Not combining constant terms correctly in the final equation.
AI-generated content may contain errors. Please verify critical information