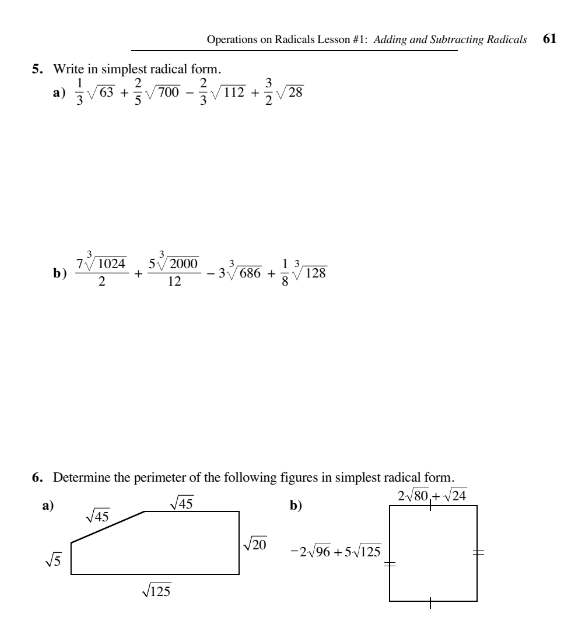
Write in simplest radical form: a) 1/3√63 + 2/5√700 - 2/3√112 + 3/2√28; b) 7/2√1024 + 5/12√2000 - 3√686 + 1/8√128. Determine the perimeter of the figures: a) √45, √45, √20, √125; b... Write in simplest radical form: a) 1/3√63 + 2/5√700 - 2/3√112 + 3/2√28; b) 7/2√1024 + 5/12√2000 - 3√686 + 1/8√128. Determine the perimeter of the figures: a) √45, √45, √20, √125; b) 2√80 + √24 - 2√96 + 5√125. Read more

Steps to Solve

1. Simplifying the terms
   First, we simplify each radical expression in the given problems.

   For part a, we start with:

   • $ \frac{1}{3} \sqrt{63} = \frac{1}{3} \cdot 3\sqrt{7} = \sqrt{7} $
   • $ \frac{2}{5} \sqrt{700} = \frac{2}{5} \cdot 10\sqrt{7} = 4\sqrt{7} $
   • $ -\frac{2}{3} \sqrt{112} = - \frac{2}{3} \cdot 4\sqrt{7} = -\frac{8}{3}\sqrt{7} $
   • $ \frac{3}{2} \sqrt{28} = \frac{3}{2} \cdot 2\sqrt{7} = 3\sqrt{7} $

   Now combine like terms:
   $$ \sqrt{7} + 4\sqrt{7} - \frac{8}{3}\sqrt{7} + 3\sqrt{7} $$

2. Finding a common denominator
   We need a common denominator to combine the coefficients of $\sqrt{7}$. The common denominator is 3:

   $$ \sqrt{7} = \frac{3}{3}\sqrt{7} $$
   $$ 4\sqrt{7} = \frac{12}{3}\sqrt{7} $$
   $$ 3\sqrt{7} = \frac{9}{3}\sqrt{7} $$

   Combining all parts gives:
   $$ \frac{3 + 12 - 8 + 9}{3} \sqrt{7} = \frac{16}{3} \sqrt{7} $$

3. Simplifying part b
   Next, simplify part b:

   • $ \frac{7}{2} \sqrt[3]{1024} = \frac{7}{2} \cdot 10 = 35 $
   • $ \frac{5}{12} \sqrt[3]{2000} = \frac{5}{12} \cdot 10 = \frac{50}{12} = \frac{25}{6} $
   • $ -3 \sqrt[3]{686} \text{ (no simplification possible, keep as is)} $
   • $ \frac{1}{8} \sqrt[3]{128} = \frac{1}{8} \cdot 8 = 1 $

   Thus, combining gives:
   $$ 35 + \frac{25}{6} - 3 \sqrt[3]{686} + 1 $$
   To combine $35 + 1$, results in:
   $$ 36 + \frac{25}{6} - 3 \sqrt[3]{686} $$

4. Calculating the perimeter
   Now let’s determine the perimeter of the geometric figures.

   For figure a, with dimensions $ \sqrt{45} \times \sqrt{45} \times \sqrt{20} \times \sqrt{125} $, the perimeter $P$ is calculated as: $$ P = 2(\sqrt{45} + \sqrt{20}) $$

   For figure b:
   The expressions to calculate perimeter:
   $$ P = 2 (\sqrt{80} + \sqrt{24}) - 2(\sqrt{96} + \sqrt{125}) $$

5. Final calculations
   Compute simplified versions of the perimeter from the two figures after simplifications.