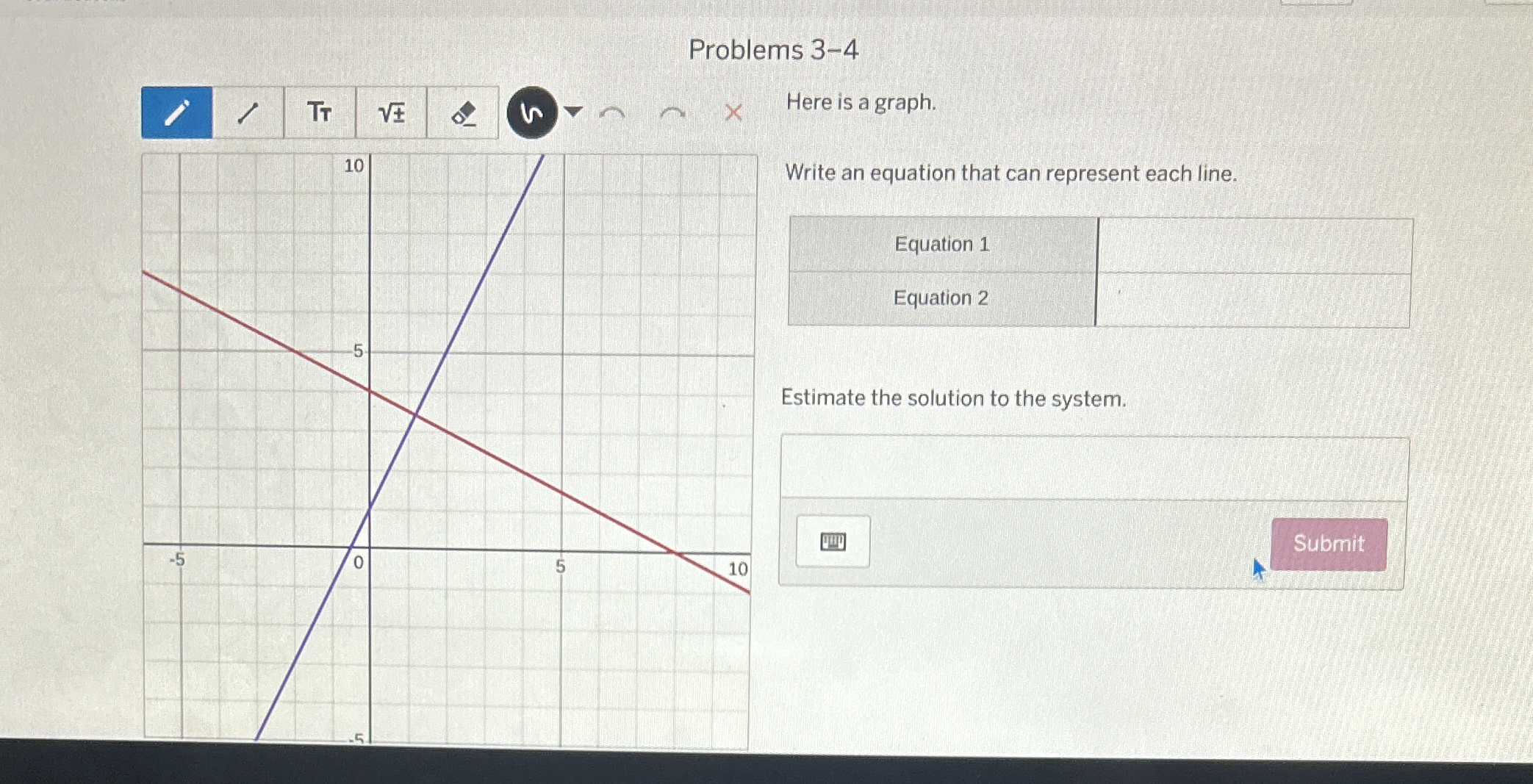
Write an equation that can represent each line. Estimate the solution to the system.

Steps to Solve

1. Identify y-intercepts of each line For the red line, it intersects the y-axis at $(0, 5)$. Thus, the y-intercept is $b_1 = 5$.

For the blue line, it intersects the y-axis at $(0, -5)$. Thus, the y-intercept is $b_2 = -5$.

2. Determine slopes of each line To find the slope (m) of each line, we can use the coordinates of two points on each line.

For the red line, passing through points $(0, 5)$ and $(5, 0)$: [ m_1 = \frac{y_2 - y_1}{x_2 - x_1} = \frac{0 - 5}{5 - 0} = -1 ]

For the blue line, passing through points $(0, -5)$ and $(5, 5)$: [ m_2 = \frac{5 - (-5)}{5 - 0} = \frac{10}{5} = 2 ]

3. Write equations of each line Using the slope-intercept form of the equation $y = mx + b$:

For the red line: [ y = -1x + 5 \quad \text{or} \quad y = -x + 5 ]

For the blue line: [ y = 2x - 5 ]

4. Estimate the solution to the system To estimate the solution, find the point of intersection formed by plugging the second equation into the first: [ -x + 5 = 2x - 5 ] Solving for $x$ gives: [ 5 + 5 = 2x + x \implies 10 = 3x \implies x \approx 3.33 ]

Substituting $x \approx 3.33$ back into one of the line equations to find $y$: [ y \approx -3.33 + 5 \approx 1.67 ]

Thus, the estimated solution is approximately $(3.33, 1.67)$.