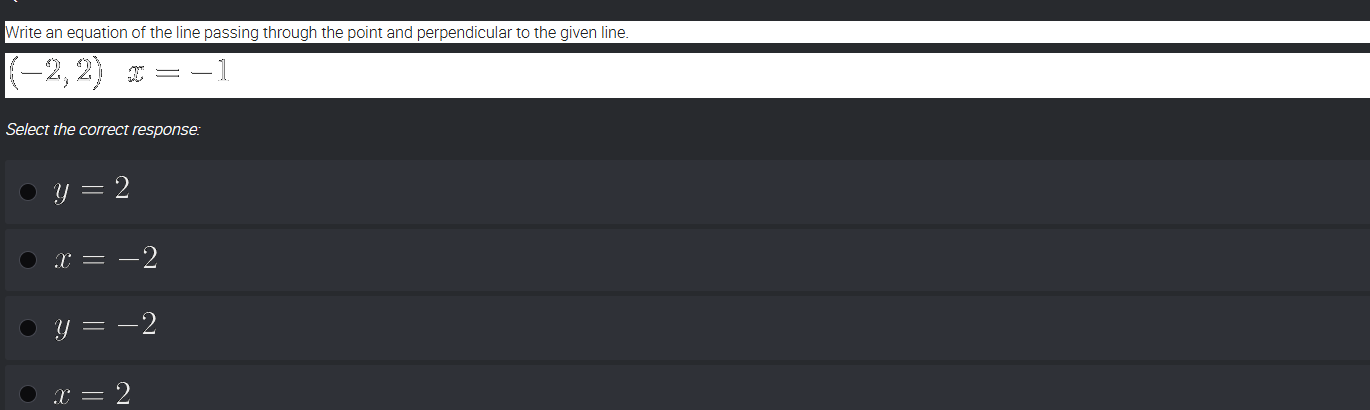
Write an equation of the line passing through the point (-2, 2) and perpendicular to the given line x = -1.
Understand the Problem
The question is asking for an equation of a line that passes through the point (-2, 2) and is perpendicular to the line defined by the equation x = -1. To solve this, we need to find the slope of the perpendicular line and then use the point-slope form to write the equation of the line.
Answer
$y = 2$
Answer for screen readers
The equation of the line is $y = 2$.
Steps to Solve
-
Identify the given line The given line is represented by the equation $x = -1$, which is a vertical line.
-
Determine the slope of the given line Since the line $x = -1$ is vertical, its slope is undefined. A line that is perpendicular to a vertical line is horizontal, which has a slope of $0$.
-
Use the point-slope form The equation of a horizontal line passing through the point $(-2, 2)$ will have the form $y = b$, where $b$ is the $y$-coordinate of the point. Here, $b = 2$.
-
Write the equation Thus, the equation of the line that is perpendicular to $x = -1$ and passes through the point $(-2, 2)$ is:
$$ y = 2 $$
The equation of the line is $y = 2$.
More Information
The line $y = 2$ is a horizontal line that intersects the y-axis at 2. It remains parallel to the x-axis for all values of $x$.
Tips
- Confusing horizontal and vertical lines: Remember that a horizontal line has a slope of $0$, while a vertical line has an undefined slope.
AI-generated content may contain errors. Please verify critical information