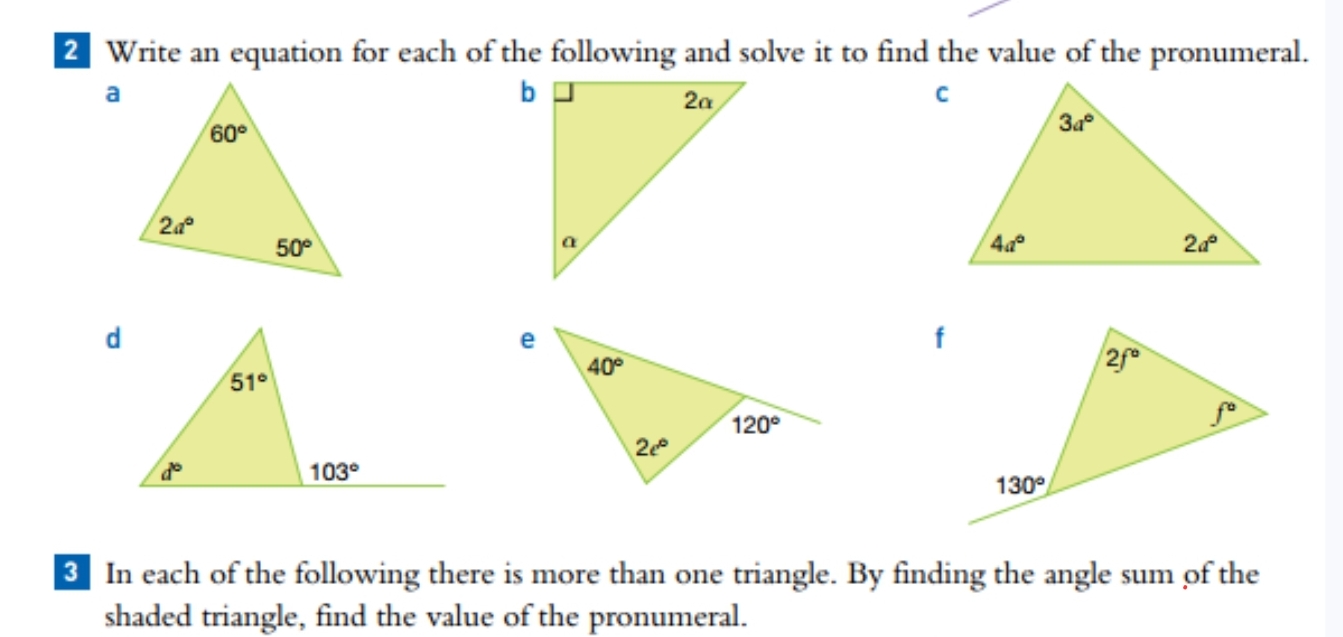
Write an equation for each of the following and solve it to find the value of the pronumeral.
Understand the Problem
The question asks for the creation of equations based on the angles in various triangles and to solve for the unknown angle represented as a pronumeral in each case. We need to apply the angle sum property (the sum of the angles in a triangle is 180 degrees) for each triangle to form equations and solve for the pronumeral.
Answer
- Triangle a: $\alpha = 35^\circ$ - Triangle b: $\alpha = 30^\circ$ - Triangle c: $\alpha = 20^\circ$ - Triangle d: $d = 26^\circ$ - Triangle e: $e = 10^\circ$ - Triangle f: $f \approx 16.67^\circ$
Answer for screen readers
- Triangle a: $\alpha = 35^\circ$
- Triangle b: $\alpha = 30^\circ$
- Triangle c: $\alpha = 20^\circ$
- Triangle d: $d = 26^\circ$
- Triangle e: $e = 10^\circ$
- Triangle f: $f \approx 16.67^\circ$
Steps to Solve
-
Triangle a: Formulate the Equation The angles in the triangle sum to 180 degrees, so we can express this as: $$ 60 + 50 + 2\alpha = 180 $$
-
Triangle a: Solve for $\alpha$ Rearranging gives: $$ 2\alpha = 180 - 110 $$ Therefore: $$ 2\alpha = 70 $$ Dividing by 2: $$ \alpha = 35 $$
-
Triangle b: Formulate the Equation The right angle is $90^\circ$, thus: $$ 90 + 2\alpha + \alpha = 180 $$
-
Triangle b: Solve for $\alpha$ Rearranging gives: $$ 3\alpha + 90 = 180 $$ Thus: $$ 3\alpha = 90 $$ Dividing by 3: $$ \alpha = 30 $$
-
Triangle c: Formulate the Equation The angles sum to 180 degrees: $$ 3\alpha + 4\alpha + 2\alpha = 180 $$
-
Triangle c: Solve for $\alpha$ Combining like terms gives: $$ 9\alpha = 180 $$ Dividing by 9: $$ \alpha = 20 $$
-
Triangle d: Formulate the Equation The sum of the angles is: $$ d + 51 + 103 = 180 $$
-
Triangle d: Solve for $d$ Rearranging gives: $$ d + 154 = 180 $$ Thus: $$ d = 26 $$
-
Triangle e: Formulate the Equation The angles sum to: $$ 40 + 120 + 2e = 180 $$
-
Triangle e: Solve for $e$ Rearranging gives: $$ 2e + 160 = 180 $$ Thus: $$ 2e = 20 $$ Dividing by 2: $$ e = 10 $$
-
Triangle f: Formulate the Equation The sum of angles in triangle f is: $$ 2f + f + 130 = 180 $$
-
Triangle f: Solve for $f$ Combining like terms gives: $$ 3f + 130 = 180 $$ Thus: $$ 3f = 50 $$ Dividing by 3: $$ f = \frac{50}{3} \approx 16.67 $$
- Triangle a: $\alpha = 35^\circ$
- Triangle b: $\alpha = 30^\circ$
- Triangle c: $\alpha = 20^\circ$
- Triangle d: $d = 26^\circ$
- Triangle e: $e = 10^\circ$
- Triangle f: $f \approx 16.67^\circ$
More Information
This problem demonstrates the application of the triangle angle sum property, which states that the angles of a triangle always add up to 180 degrees. By carefully setting up an equation for each triangle and solving for the unknown variable, we can easily find the missing angles.
Tips
- Failing to recognize that a right angle equals $90^\circ$ in triangle b.
- Miscalculating the sums when combining angles.
- Forgetting to account for all angles in the triangles, which might lead to incorrect equations.
AI-generated content may contain errors. Please verify critical information