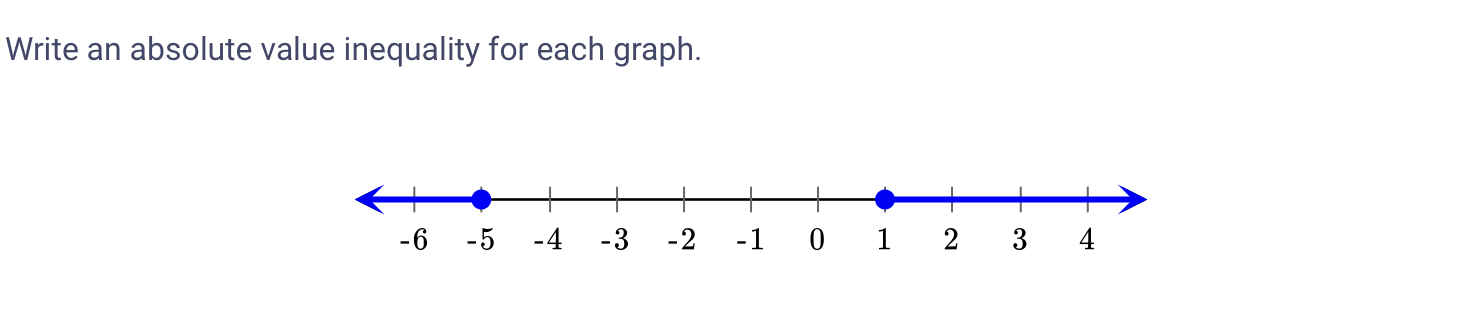
Write an absolute value inequality for each graph.
Understand the Problem
The question is asking for an absolute value inequality that corresponds to the provided graph on a number line. This requires interpreting the graph to identify the center point and the direction of the inequality.
Answer
The absolute value inequality is $$ |x + 5| \geq 0 $$
Answer for screen readers
The absolute value inequality corresponding to the graph is
$$ |x + 5| \geq 0 $$
Steps to Solve
-
Identify the Center Point
The first step is to determine the center point of the graph. In the provided graph, the solid dot is located at $-5$. This indicates the center of the absolute value inequality. -
Determine the Direction of the Inequality
Next, we observe that the line extends to the left from $-5$ and continues infinitely. This suggests that the absolute value inequality will be of the form $|x - (-5)| \geq k$ where $k$ is a positive number representing the distance. -
Define the Inequality
From the graph, we can see that it includes all values less than $-5$. This gives us the inequality $|x + 5| \geq 0$. Since the line goes infinitely left, we choose a specific distance. For example, if we take $k = 0$ to represent this direction adequately, our inequality becomes:
$$ |x + 5| \geq 0 $$
The absolute value inequality corresponding to the graph is
$$ |x + 5| \geq 0 $$
More Information
This inequality represents all numbers $x$ that are less than or equal to $-5$. The absolute value notation captures both directions from the center point, allowing for the expression of the entire region on the number line.
Tips
- Choosing the Wrong Direction: A common mistake is to misinterpret the direction of the inequality. Always pay attention to whether the line continues to the left or expands to the right.
- Incorrect Center Point: Ensure that you correctly identify the center point on the number line; mixed up placement can lead to erroneous inequalities.
AI-generated content may contain errors. Please verify critical information