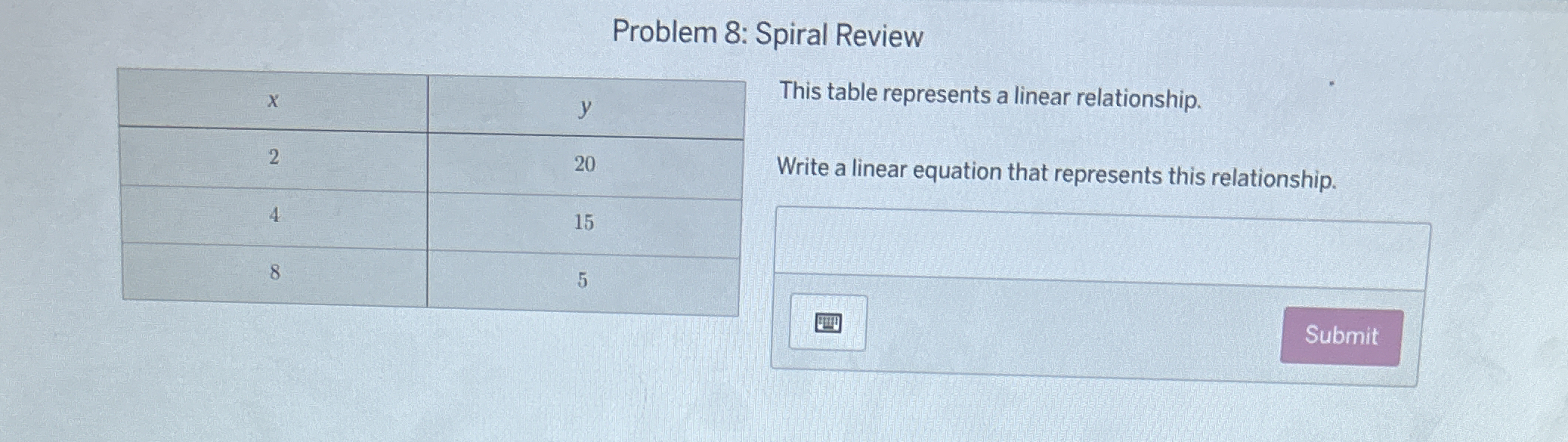
Write a linear equation that represents the linear relationship in the provided table.
Understand the Problem
The question is asking to identify the linear relationship between the given values of x and y in the table and to write a linear equation that represents this relationship.
Answer
$$ y = -\frac{5}{2}x + 25 $$
Answer for screen readers
The linear equation that represents the relationship is:
$$ y = -\frac{5}{2}x + 25 $$
Steps to Solve
- Identify the points from the table
From the table, we have the following points:
- (2, 20)
- (4, 15)
- (8, 5)
- Calculate the slope (m)
Use the formula for the slope between two points $(x_1, y_1)$ and $(x_2, y_2)$:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Using the points (2, 20) and (4, 15):
$$ m = \frac{15 - 20}{4 - 2} = \frac{-5}{2} = -\frac{5}{2} $$
- Use point-slope form to find the equation
Point-slope form of a linear equation is given by:
$$ y - y_1 = m(x - x_1) $$
Using point (2, 20) and the calculated slope:
$$ y - 20 = -\frac{5}{2}(x - 2) $$
- Simplify to slope-intercept form (y = mx + b)
Distributing on the right side:
$$ y - 20 = -\frac{5}{2}x + 5 $$
Add 20 to both sides:
$$ y = -\frac{5}{2}x + 25 $$
The linear equation that represents the relationship is:
$$ y = -\frac{5}{2}x + 25 $$
More Information
This equation indicates that for every increase of 1 in $x$, $y$ decreases by $\frac{5}{2}$, and when $x$ is 0, $y$ equals 25. This shows a linear decline.
Tips
- Forgetting to calculate the slope between different pairs of points, leading to incorrect slope values.
- Not correctly substituting the points into the point-slope form leading to errors in the final equation.
AI-generated content may contain errors. Please verify critical information