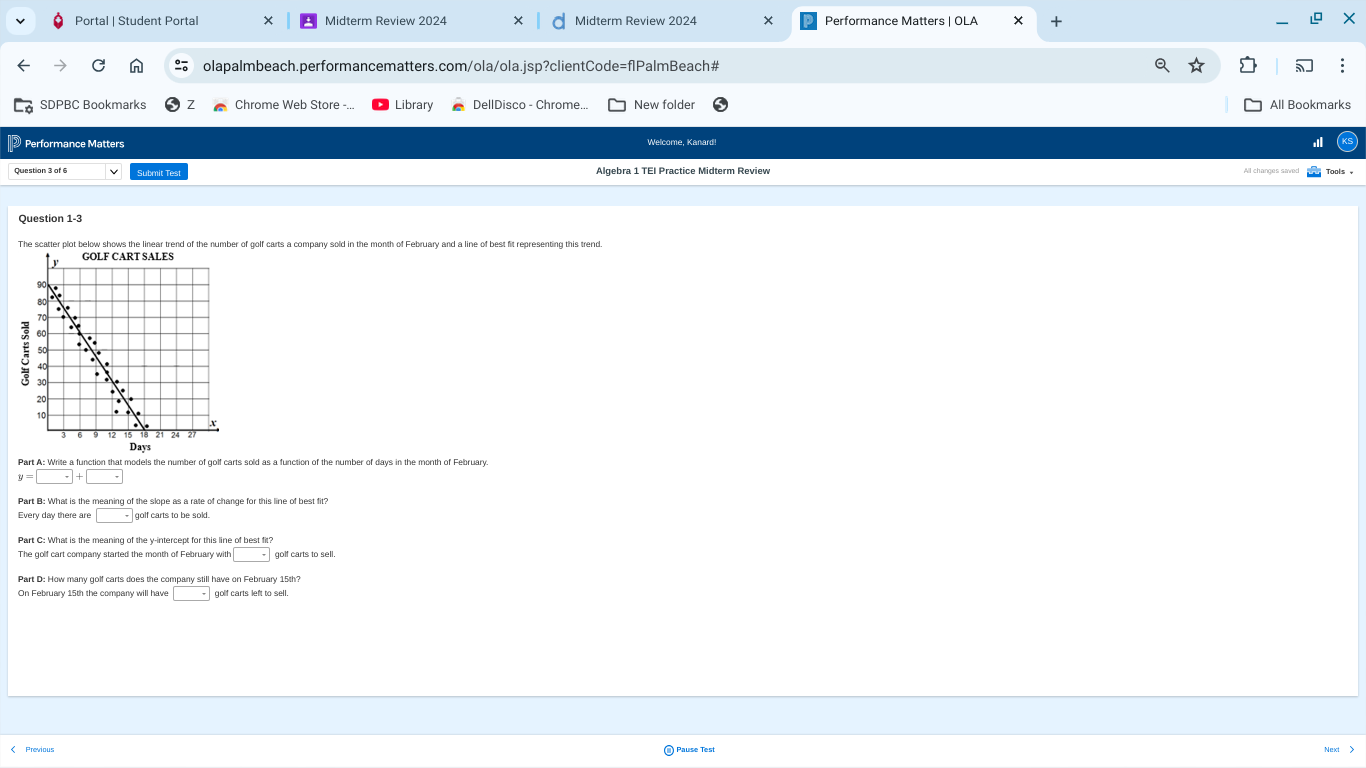
Write a function that models the number of golf carts sold as a function of the number of days in the month of February. What is the meaning of the slope as a rate of change for th... Write a function that models the number of golf carts sold as a function of the number of days in the month of February. What is the meaning of the slope as a rate of change for this line of best fit? What is the meaning of the y-intercept? How many golf carts does the company still have on February 15th? Read more

Steps to Solve

1. Identify the Linear Function We need to find a linear function to model the golf carts sold based on the data shown in the scatter plot. A linear function typically has the form:

$$ y = mx + b $$

Here, $y$ represents the number of golf carts sold, $x$ represents the number of days into February, $m$ is the slope, and $b$ is the y-intercept.

2. Determine the Slope ($m$) From the scatter plot, determine two points from the line of best fit. For example, if a point is at (3, 15) and another at (9, 0):

The slope $m$ can be calculated using the formula:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Plugging in our points: $$ m = \frac{0 - 15}{9 - 3} = \frac{-15}{6} = -2.5 $$

This means the slope is $-2.5$, so every day, 2.5 fewer golf carts are sold.

3. Find the Y-Intercept ($b$) The y-intercept is the value of $y$ when $x = 0$. From the plot, if the y-intercept shows 21 golf carts when no days have passed, then:

$$ b = 21 $$

4. Write the Final Equation Now we can write the complete linear function combining the slope and y-intercept:

$$ y = -2.5x + 21 $$

5. Interpret the Slope As previously calculated, the slope represents the rate of change of golf cart sales:

Every day, roughly 2.5 fewer golf carts are sold.

6. Interpret the Y-Intercept The y-intercept, 21, indicates the number of golf carts available at the start of February (Day 0).

7. Predict Sales on February 15 To find out how many carts are left on February 15 ($x = 15$):

$$ y = -2.5(15) + 21 $$

Calculating this will give us the remaining golf carts.