Write 1 + 64x^3 in factored form.
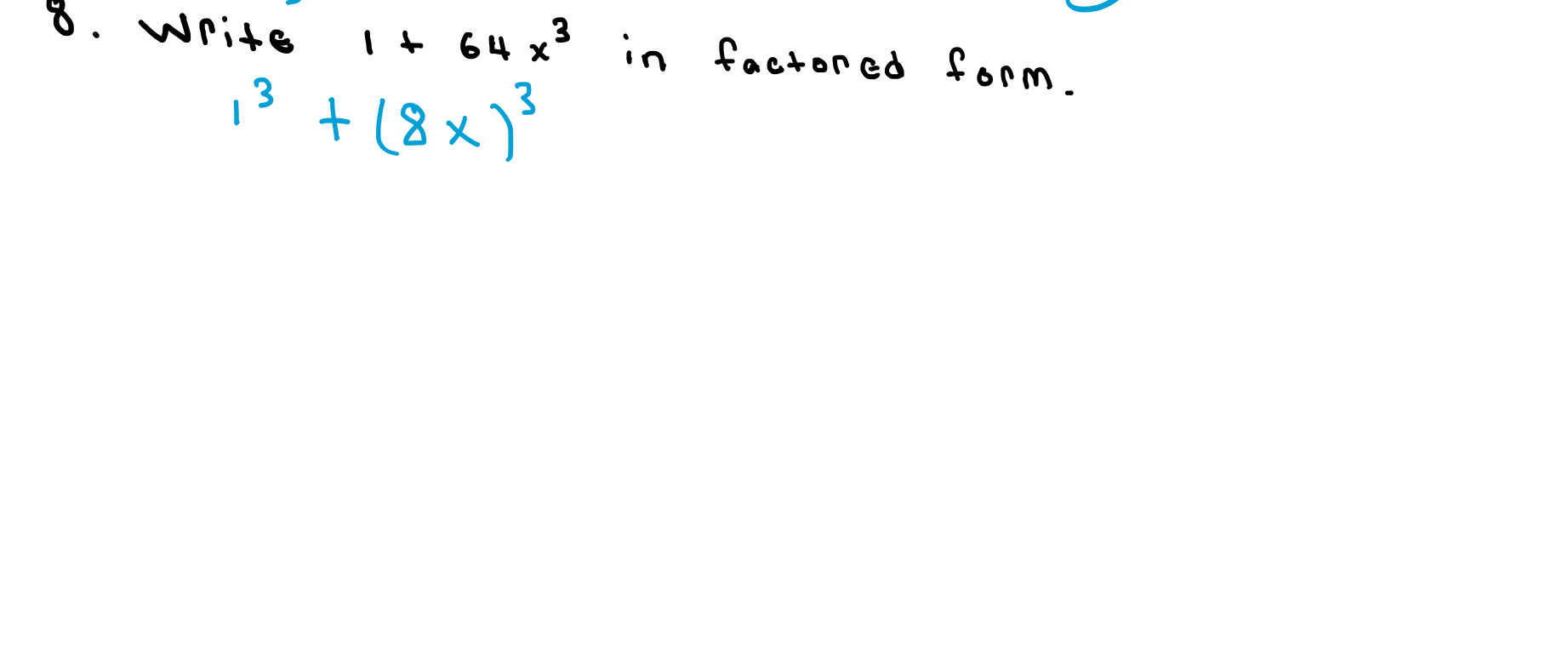
Understand the Problem
The question is asking to factor the expression 1^3 + (8x)^3. This involves recognizing that it can be simplified using the sum of cubes formula.
Answer
The factored form is $$(1 + 8x)(1 - 8x + 64x^2)$$.
Answer for screen readers
The factored form of (1^3 + (8x)^3) is $$(1 + 8x)(1 - 8x + 64x^2)$$
Steps to Solve
- Identify the sum of cubes formula
The sum of cubes formula is given by: $$ a^3 + b^3 = (a + b)(a^2 - ab + b^2) $$
- Assign values to a and b
In this expression (1^3 + (8x)^3), we can identify:
- ( a = 1 )
- ( b = 8x )
- Calculate a², ab, and b²
Now substitute (a) and (b) into the formula:
- ( a^2 = 1^2 = 1 )
- ( ab = 1 \cdot (8x) = 8x )
- ( b^2 = (8x)^2 = 64x^2 )
- Substitute the values into the formula
Now substitute ( a ) and ( b ) along with their calculated values into the sum of cubes formula: $$ 1^3 + (8x)^3 = (1 + 8x)(1 - 8x + 64x^2) $$
The factored form of (1^3 + (8x)^3) is $$(1 + 8x)(1 - 8x + 64x^2)$$
More Information
Factoring expressions using the sum of cubes is a useful technique in algebra. Understanding how to manipulate these formulas can help simplify complex expressions and solve equations more efficiently.
Tips
- Forgetting to apply the sum of cubes formula: Always check if the expression fits the sum of cubes format before trying to factor.
- Incorrect calculations of (a^2), (ab), and (b^2): Ensure each calculation is accurate to avoid incorrect factoring.
AI-generated content may contain errors. Please verify critical information