Work out the values of t and w in the equalities below. a) 18^t / 18^15 = 18^5
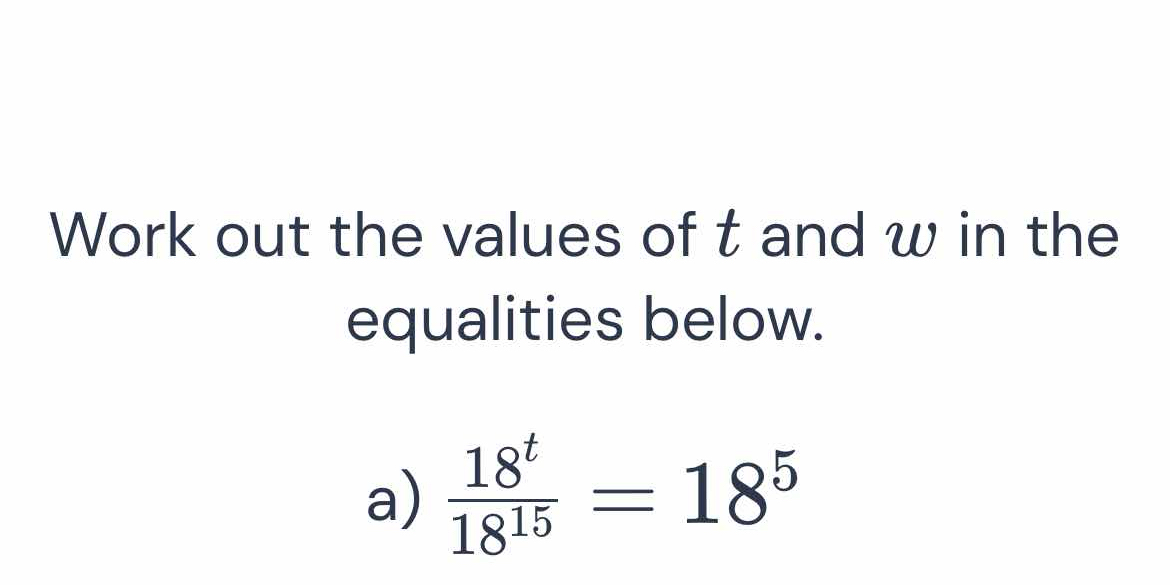
Understand the Problem
The question is asking to solve for the values of t and w in the given mathematical equations involving exponents and bases. It requires applying the properties of exponents to simplify the equation provided.
Answer
The value of $t$ is $20$.
Answer for screen readers
The value of $t$ is $20$.
Steps to Solve
- Rewrite the fraction using properties of exponents
The property of exponents we use is
$$ \frac{a^m}{a^n} = a^{m-n} $$
Applying this to the equation gives:
$$ \frac{18^t}{18^{15}} = 18^{t-15} $$
- Set the exponents equal to each other
Since the bases are the same (both are 18), we can set the exponents equal:
$$ t - 15 = 5 $$
- Solve for $t$
To isolate $t$, add 15 to both sides:
$$ t = 5 + 15 $$
- Calculate the value of $t$
This gives:
$$ t = 20 $$
The value of $t$ is $20$.
More Information
This problem involves using the properties of exponents. Since the bases were the same, we could directly set the exponents equal and solve for the unknown.
Tips
- Forgetting to apply the property of exponents properly. Make sure to understand that we can subtract exponents when dividing powers with the same base.
- Not setting the exponents equal after simplifying the expression.
AI-generated content may contain errors. Please verify critical information