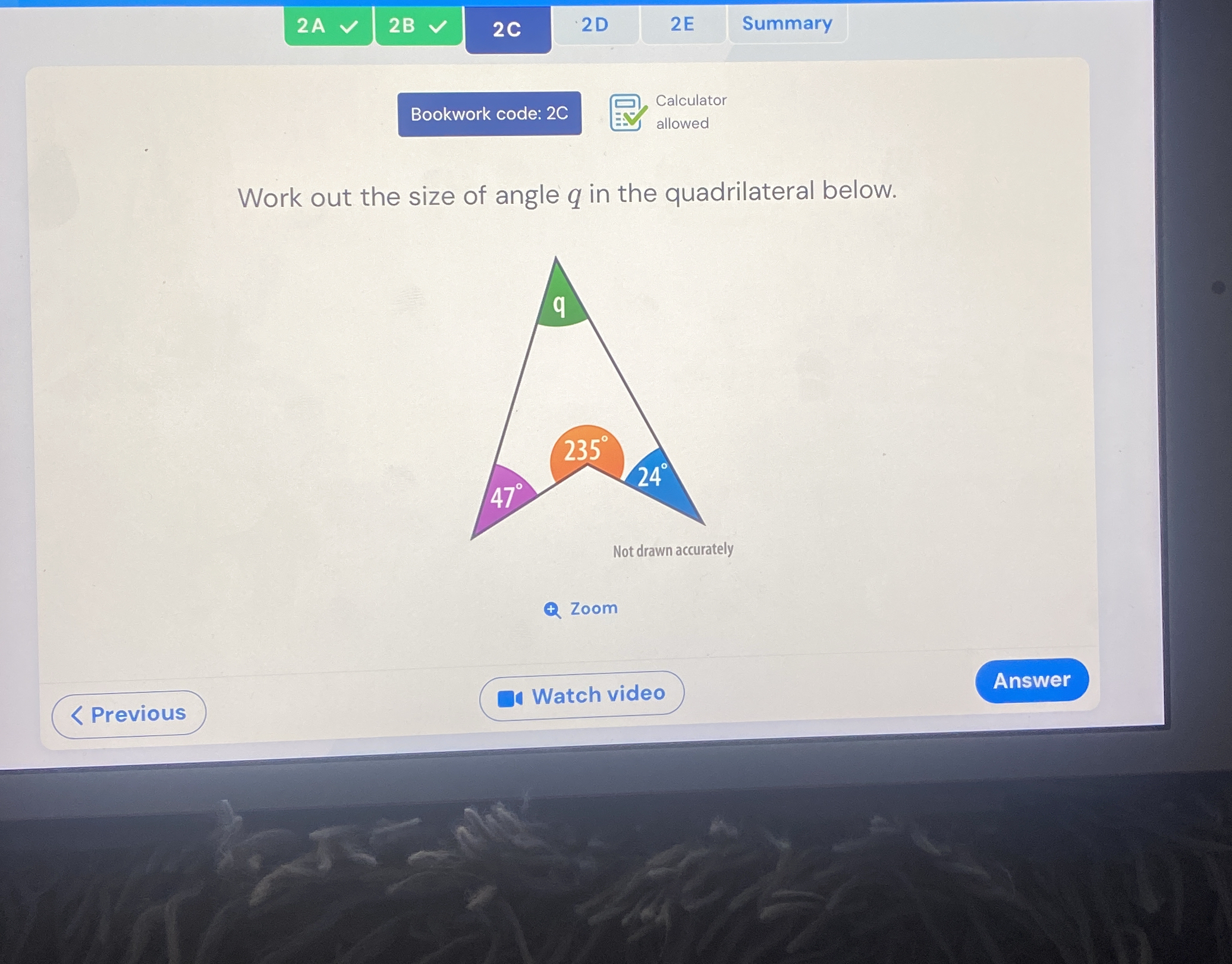
Work out the size of angle q in the quadrilateral below.
Understand the Problem
The question is asking us to calculate the size of angle q in a quadrilateral where the other three angles are given. We will use the property that the sum of interior angles in a quadrilateral is 360 degrees to find the missing angle.
Answer
The size of angle $q$ is $54^\circ$.
Answer for screen readers
The size of angle $q$ is $54^\circ$.
Steps to Solve
-
Identify the sum of angles in a quadrilateral The sum of the interior angles in a quadrilateral is always $360^\circ$.
-
List given angles The angles provided are $235^\circ$, $24^\circ$, and $47^\circ$.
-
Calculate the sum of the known angles Add the known angles together: $$ 235^\circ + 24^\circ + 47^\circ = 306^\circ $$
-
Determine the measure of angle q Subtract the sum of the known angles from $360^\circ$ to find angle $q$: $$ q = 360^\circ - 306^\circ $$
-
Calculate q Perform the subtraction: $$ q = 54^\circ $$
The size of angle $q$ is $54^\circ$.
More Information
In any quadrilateral, the sum of all interior angles is $360^\circ$. Understanding this property allows us to find missing angles by simple arithmetic.
Tips
- Forgetting the sum rule: Sometimes students forget that the total needs to equal $360^\circ$.
- Incorrect addition: Ensure that when adding angles, all angles are accurately summed before subtracting from $360^\circ$.
AI-generated content may contain errors. Please verify critical information