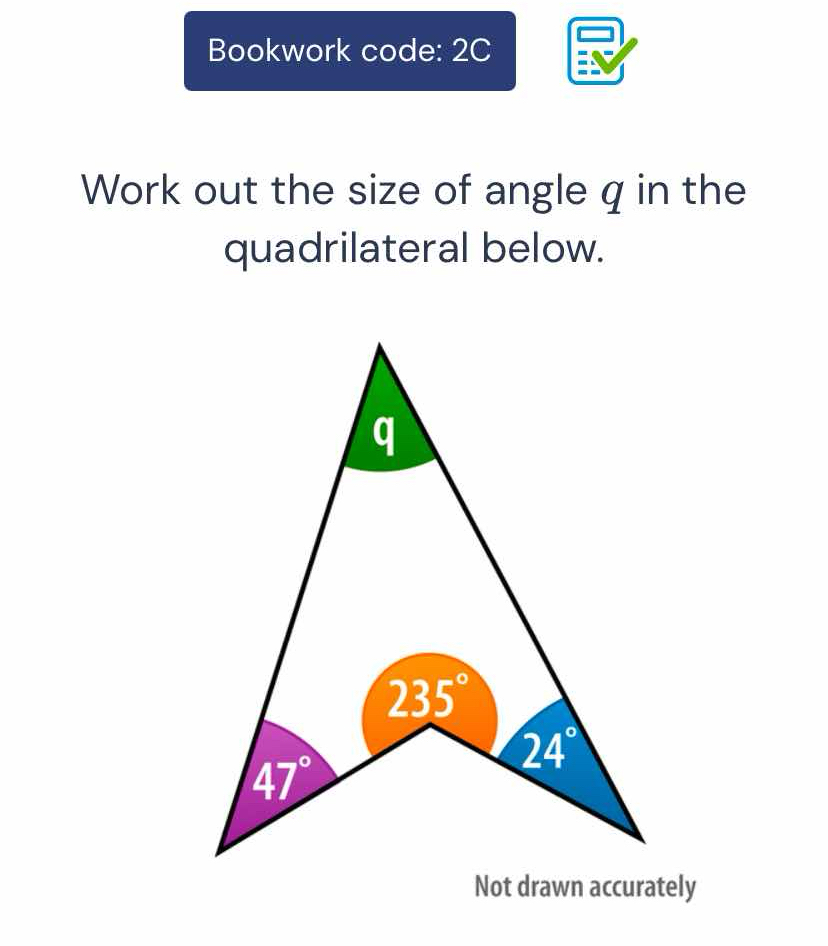
Work out the size of angle q in the quadrilateral below.
Understand the Problem
The question is asking to calculate the size of angle q in a quadrilateral, given three other angles, one of which is 235°, and the others are 47° and 24°. To solve this, we will use the fact that the total sum of angles in a quadrilateral is 360°.
Answer
The size of angle $q$ is $54^\circ$.
Answer for screen readers
The size of angle $q$ is $54^\circ$.
Steps to Solve
-
Understand the total angle sum of a quadrilateral The total sum of the angles in a quadrilateral is $360^\circ$.
-
Add the known angles We need to add the three known angles: $$ 235^\circ + 47^\circ + 24^\circ $$
-
Calculate the sum of the known angles Calculate the total of the known angles: $$ 235 + 47 + 24 = 306^\circ $$
-
Subtract the sum from 360° To find angle $q$, we subtract the total of the known angles from $360^\circ$: $$ q = 360^\circ - 306^\circ $$
-
Calculate angle q Now, perform the subtraction: $$ q = 54^\circ $$
The size of angle $q$ is $54^\circ$.
More Information
In any quadrilateral, the sum of the interior angles always equals $360^\circ$. This property is fundamental in geometry.
Tips
- Forgetting the total angle sum of a quadrilateral, which is $360^\circ$.
- Adding the angles incorrectly. Always double-check your addition.
AI-generated content may contain errors. Please verify critical information