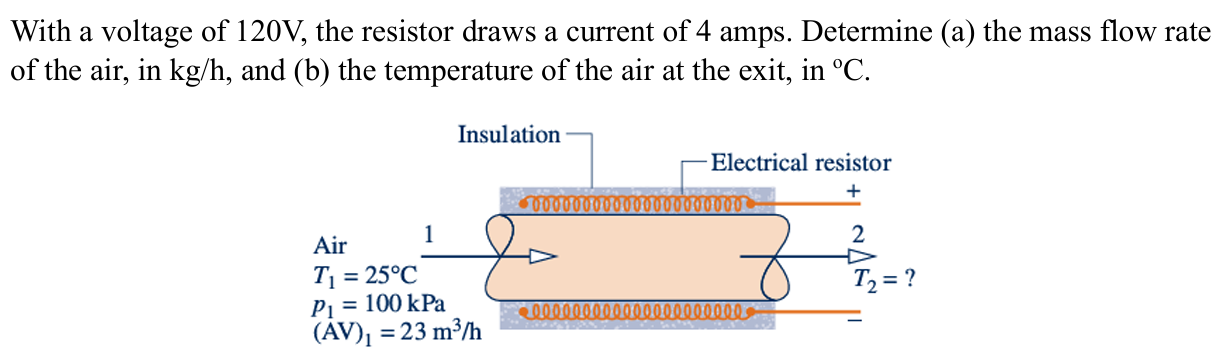
With a voltage of 120V, the resistor draws a current of 4 amps. Determine (a) the mass flow rate of the air, in kg/h, and (b) the temperature of the air at the exit, in °C.
Understand the Problem
The question is asking us to calculate two things: (a) the mass flow rate of air in kg/h, and (b) the temperature of the air at the exit of the electrical resistor. We will use principles from thermodynamics and fluid mechanics to solve these problems based on the given parameters.
Answer
The mass flow rate is $23 \, \text{kg/h}$ and the exit temperature is $41 \, \text{°C}$.
Answer for screen readers
(a) The mass flow rate of air is ( \dot{m} \approx 23 , \text{kg/h} ).
(b) The temperature of the air at the exit is ( T_2 \approx 41 , \text{°C} ).
Steps to Solve
-
Calculate the power of the resistor To find the power (in watts) consumed by the resistor, use the formula: $$ P = V \times I $$ where ( V = 120 , \text{V} ) and ( I = 4 , \text{A} ).
-
Determine the temperature rise of the air To find the temperature change of the air as it passes through the resistor, we assume all the power goes into heating the air. We use the specific heat formula: $$ Q = mc\Delta T $$ where ( Q = P ) (from Step 1), ( m ) is the mass flow rate in kg/s, and ( c = 1005 , \text{J/(kg} \cdot \text{K)} ) (specific heat of air).
-
Calculate the mass flow rate Using the volumetric flow rate given ( (AV)_1 = 23 , \text{m}^3/\text{h} ), we first convert this to kg/s. The density of air at standard conditions is approximately ( 1.2 , \text{kg/m}^3 ): $$ \dot{m} = \rho \times (AV)_1 $$ Convert ( (AV)_1 ) from m³/h to m³/s by dividing by 3600.
-
Calculate the final mass flow rate in kg/h Convert the mass flow rate obtained in kg/s to kg/h by multiplying by 3600.
-
Calculate the exit temperature ( T_2 ) Using the temperature rise from the power equation, we can find the exit temperature using: $$ T_2 = T_1 + \Delta T $$
-
Substituting values to solve Put in the known values to calculate the necessary terms at each stage.
(a) The mass flow rate of air is ( \dot{m} \approx 23 , \text{kg/h} ).
(b) The temperature of the air at the exit is ( T_2 \approx 41 , \text{°C} ).
More Information
The calculations are based on basic principles of thermodynamics where the power supplied to the resistor heats the air passing through it. The specific heat of air is critical in determining the temperature change.
Tips
- Forgetting to convert units properly, especially when changing between kg/h and kg/s.
- Not properly accounting for the specific heat of air, which can lead to incorrect temperature calculations.
AI-generated content may contain errors. Please verify critical information