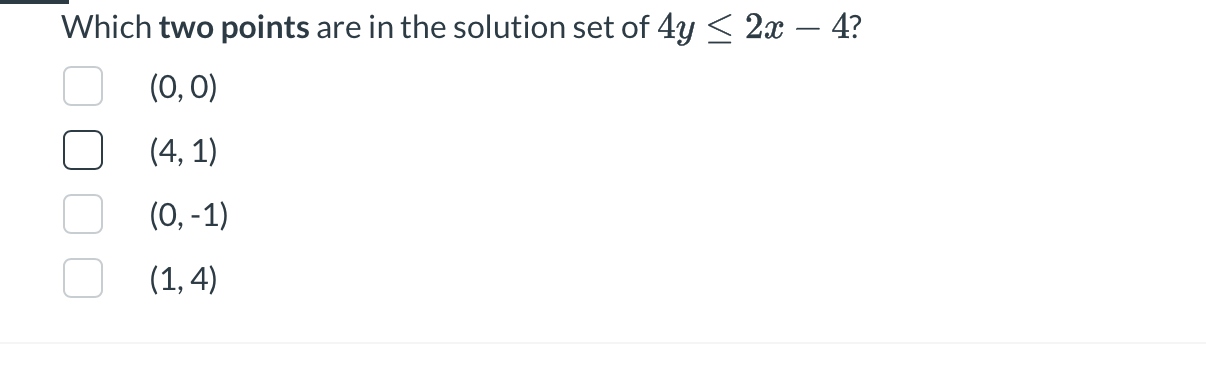
Which two points are in the solution set of 4y ≤ 2x - 4?

Steps to Solve

1. Rewrite the inequality
   We start with the inequality to analyze it:
   $$ 4y \leq 2x - 4 $$
   To simplify our checks, we can express it as:
   $$ y \leq \frac{1}{2}x - 1 $$

2. Substituting the points
   We will substitute each point into the simplified inequality and check if it holds true.

3. Check point (0, 0)
   Substituting $x = 0$ and $y = 0$:
   $$ 0 \leq \frac{1}{2}(0) - 1 $$
   $$ 0 \leq -1 \quad \text{(False)} $$

4. Check point (4, 1)
   Substituting $x = 4$ and $y = 1$:
   $$ 1 \leq \frac{1}{2}(4) - 1 $$
   $$ 1 \leq 2 - 1 $$
   $$ 1 \leq 1 \quad \text{(True)} $$

5. Check point (0, -1)
   Substituting $x = 0$ and $y = -1$:
   $$ -1 \leq \frac{1}{2}(0) - 1 $$
   $$ -1 \leq -1 \quad \text{(True)} $$

6. Check point (1, 4)
   Substituting $x = 1$ and $y = 4$:
   $$ 4 \leq \frac{1}{2}(1) - 1 $$
   $$ 4 \leq 0 - 1 $$
   $$ 4 \leq -1 \quad \text{(False)} $$

7. Identify valid points
   The points that satisfy the inequality are:

• (4, 1)
• (0, -1)