(√45)(√20)
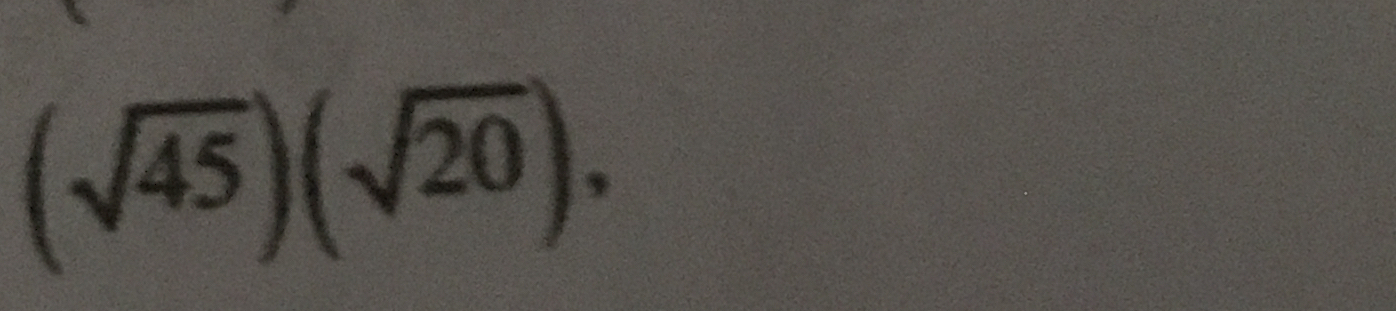
Understand the Problem
The question involves the multiplication of two square roots, specifically the square roots of 45 and 20. To solve this, we will apply the properties of square roots to simplify the expression.
Answer
The answer is $30$.
Answer for screen readers
The final answer is $30$.
Steps to Solve
-
Combine the square roots We can use the property of square roots that states $\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}$. So, we can combine the multiplication of the two square roots: $$ \sqrt{45} \cdot \sqrt{20} = \sqrt{45 \cdot 20} $$
-
Calculate the product inside the square root Next, we calculate the product of 45 and 20: $$ 45 \cdot 20 = 900 $$
-
Simplify the square root Now we can simplify the square root of 900: $$ \sqrt{900} = 30 $$
-
Final result Thus, the final answer to the problem is: $$ (\sqrt{45})(\sqrt{20}) = 30 $$
The final answer is $30$.
More Information
The product of the square roots can often lead to a simpler calculation, and in this case, it resulted in a perfect square, allowing for an easy simplification.
Tips
- Forgetting to use the property of square roots could lead to an incorrect interpretation of the expression.
- Miscalculating the product $45 \cdot 20$ can lead to errors in finding the square root.
AI-generated content may contain errors. Please verify critical information