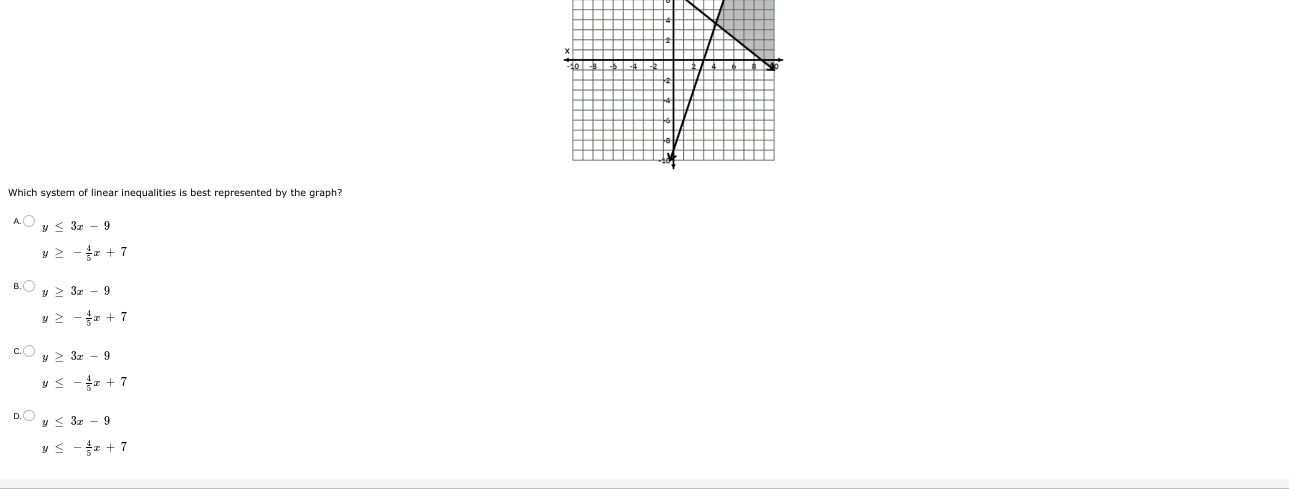
Which system of linear inequalities is best represented by the graph?
Understand the Problem
The question is asking which system of linear inequalities is represented by the given graph. We need to analyze the graph and the listed options to determine which inequalities match the shaded region depicted.
Answer
C: $$ y \geq 3x - 9 $$ $$ y \leq -\frac{4}{5}x + 7 $$
Answer for screen readers
The correct answer is C:
$$ y \geq 3x - 9 $$
$$ y \leq -\frac{4}{5}x + 7 $$
Steps to Solve
-
Identify the lines from the graph
Analyze the lines shown in the graph. There are two lines. The first has a steeper positive slope, and the second has a smaller negative slope. -
Determine the equations of the lines
The line represented by the equation $y = 3x - 9$ has a positive slope of 3.
The line represented by the equation $y = -\frac{4}{5}x + 7$ has a negative slope of $-\frac{4}{5}$. -
Analyze the shaded region
Determine where the shaded region lies in relation to the lines. If the region is above a line, the corresponding inequality would use “greater than or equal to” (≥), and if it's below, it would use “less than or equal to” (≤). -
Match the inequalities to the graph
Compare the identified regions with the options given:
- If the region above $y = 3x - 9$, then the inequality is $y \geq 3x - 9$.
- If the region below $y = -\frac{4}{5}x + 7$, then the inequality is $y \leq -\frac{4}{5}x + 7$.
-
Identify the correct system of inequalities
Check the options provided to find a match with the identified inequalities from the graph:
- If Option C states $y \geq 3x - 9$ and $y \leq -\frac{4}{5}x + 7$, it represents the correct system.
The correct answer is C:
$$ y \geq 3x - 9 $$
$$ y \leq -\frac{4}{5}x + 7 $$
More Information
This answer indicates that the shaded region is bounded above by the line with a negative slope and below by the line with a positive slope. These linear inequalities help define the area represented in the graph.
Tips
- Confusing the direction of the inequalities based on the position of the shaded region. Always check whether the region is above or below the line.
- Not considering the endpoint nature of the lines (solid vs. dashed lines) to determine whether to use "≥" or ">" and "≤" or "<".
AI-generated content may contain errors. Please verify critical information