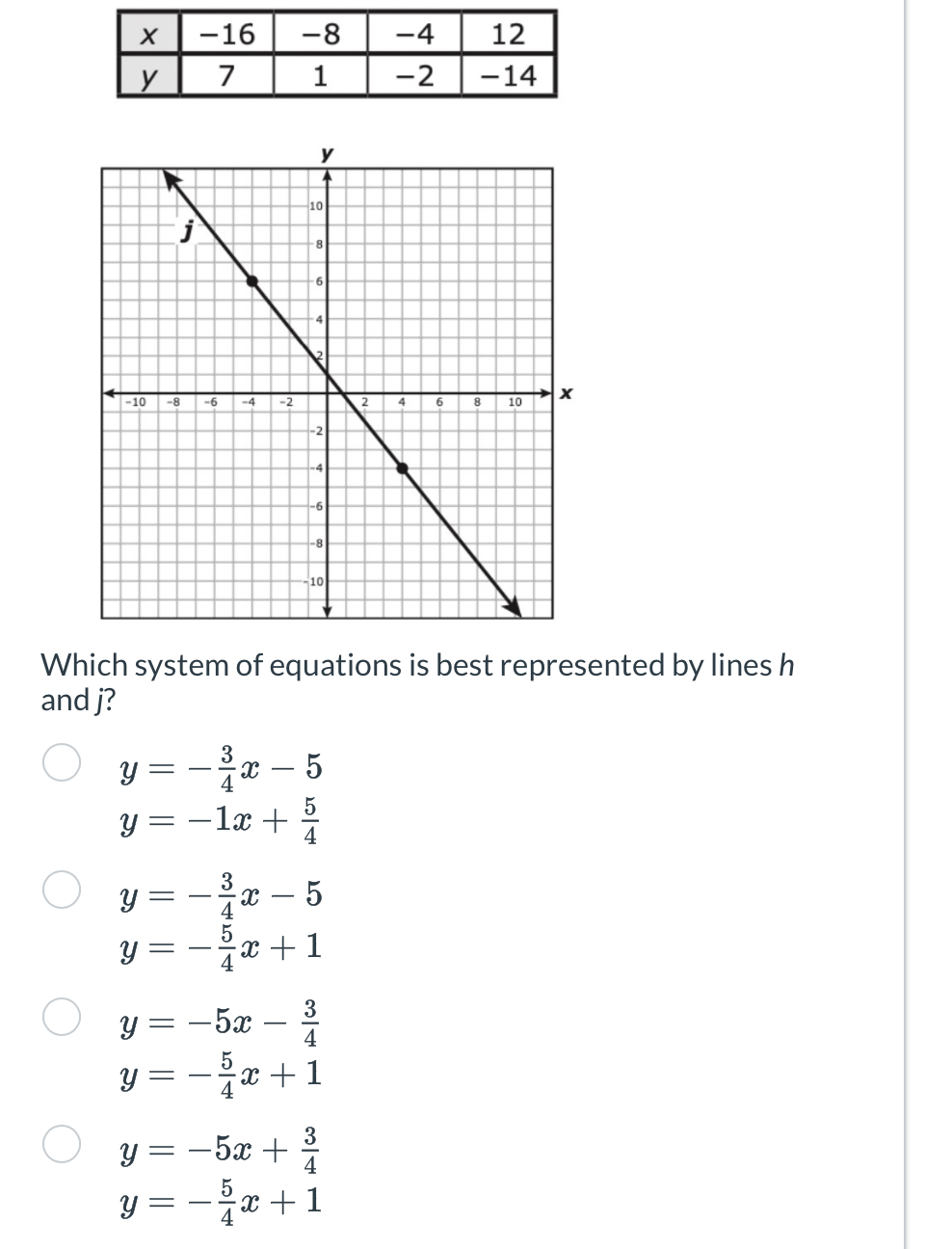
Which system of equations is best represented by lines h and j?

Steps to Solve

1. Identify Points from the Table

From the provided table, the points are:

• P1: $(-16, 7)$
• P2: $(-8, 1)$
• P3: $(-4, -2)$
• P4: $(12, -14)$

2. Determine the Slope of the Lines

To find the slope (m) of the line, use two points. Let's use points P2 and P3: $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-2 - 1}{-4 - (-8)} = \frac{-3}{4} = -\frac{3}{4} $$

3. Write the Equation of Line j (Using Point-Slope Form)

Using the slope $-\frac{3}{4}$ and point P2 $(-8, 1)$: $$ y - y_1 = m(x - x_1) $$ Substituting in the values: $$ y - 1 = -\frac{3}{4}(x + 8) $$ Expanding: $$ y - 1 = -\frac{3}{4}x - 6 $$ So, $$ y = -\frac{3}{4}x - 5 $$

4. Identify the Equation of Line h

To find line h, we check the remaining points from the table. We can use point P3 and P4 to find the slope: $$ m = \frac{-14 - (-2)}{12 - (-4)} = \frac{-12}{16} = -\frac{3}{4} $$ Using point P3 $(-4, -2)$ with the same slope: $$ y + 2 = -\frac{5}{4}(x + 4) $$ Expanding: $$ y + 2 = -\frac{5}{4}x - 5 $$ So, $$ y = -\frac{5}{4}x - 3 $$

5. Match with Given Options

Now let's match these equations with the options provided. The correct equations closely resemble:

• $y = -\frac{3}{4}x - 5$ for line j
• $y = -\frac{5}{4}x + 1$ for line h

These align with the option provided.