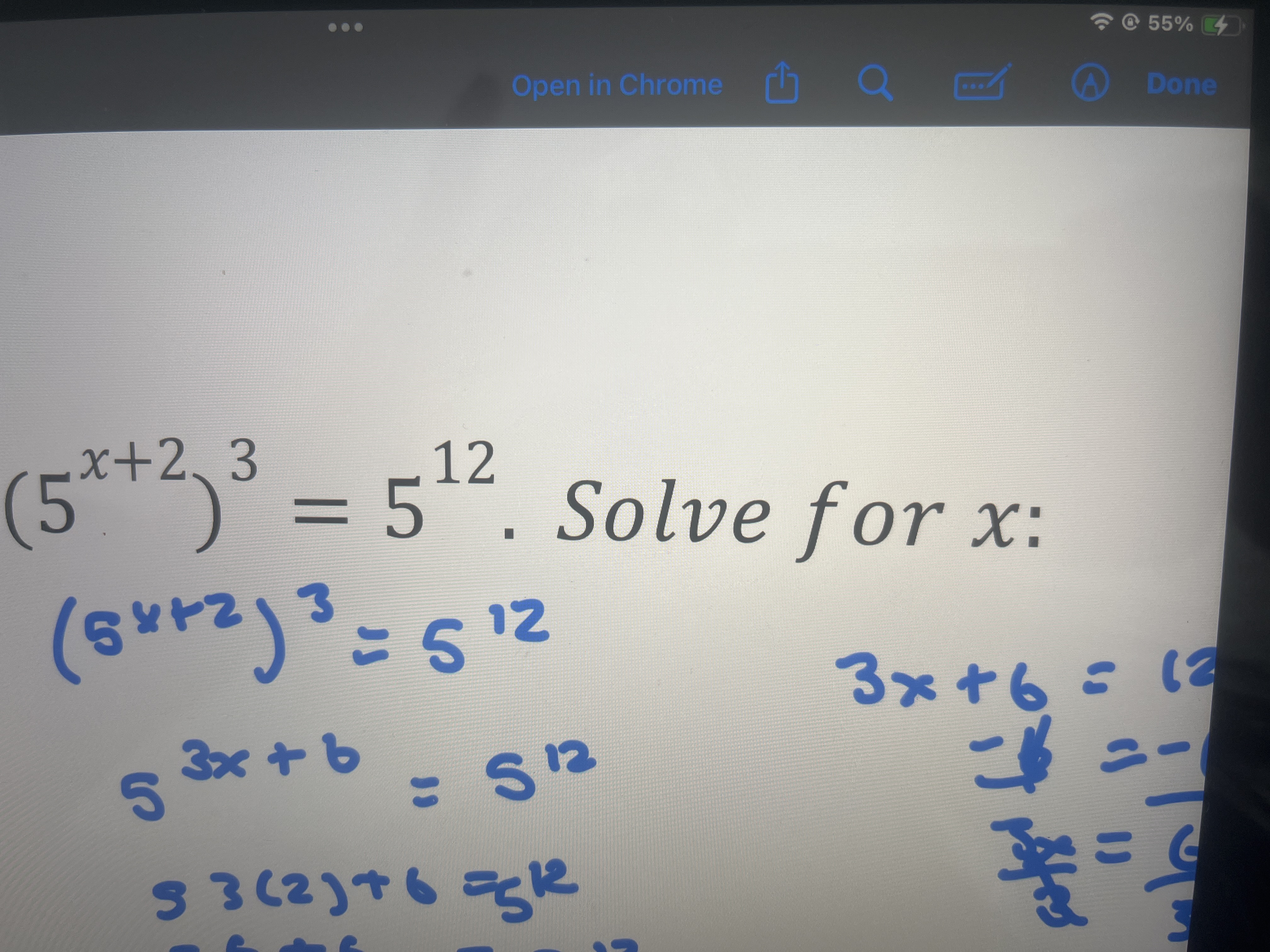
Solve for x: (5^(x+2))^3 = 5^12
Understand the Problem
The question is asking to solve the equation (5^(x+2))^3 = 5^12 for the variable x. This involves using properties of exponents to simplify and isolate x.
Answer
The value of \(x\) is \(2\).
Answer for screen readers
The solution for (x) is (x = 2).
Steps to Solve
- Apply the Power of a Power Property
Using the property of exponents, we can rewrite the left-hand side of the equation:
$$(5^{x+2})^3 = 5^{3(x+2)}$$
So the equation becomes:
$$5^{3(x+2)} = 5^{12}$$
- Set the Exponents Equal
Since the bases are the same, we can set the exponents equal to each other:
$$3(x+2) = 12$$
- Distribute the 3
Distribute the (3) on the left-hand side:
$$3x + 6 = 12$$
- Isolate the Variable
Subtract (6) from both sides to isolate the term with (x):
$$3x = 12 - 6$$
$$3x = 6$$
- Solve for (x)
Finally, divide both sides by (3) to solve for (x):
$$x = \frac{6}{3} = 2$$
The solution for (x) is (x = 2).
More Information
This equation uses the properties of exponents, specifically the power of a power property and the fact that if two exponential expressions with the same base are equal, then their exponents must also be equal.
Tips
- Misapplying the power rules, such as failing to distribute the exponent correctly when applying the power of a power property.
- Forgetting to isolate the variable completely before dividing.
AI-generated content may contain errors. Please verify critical information