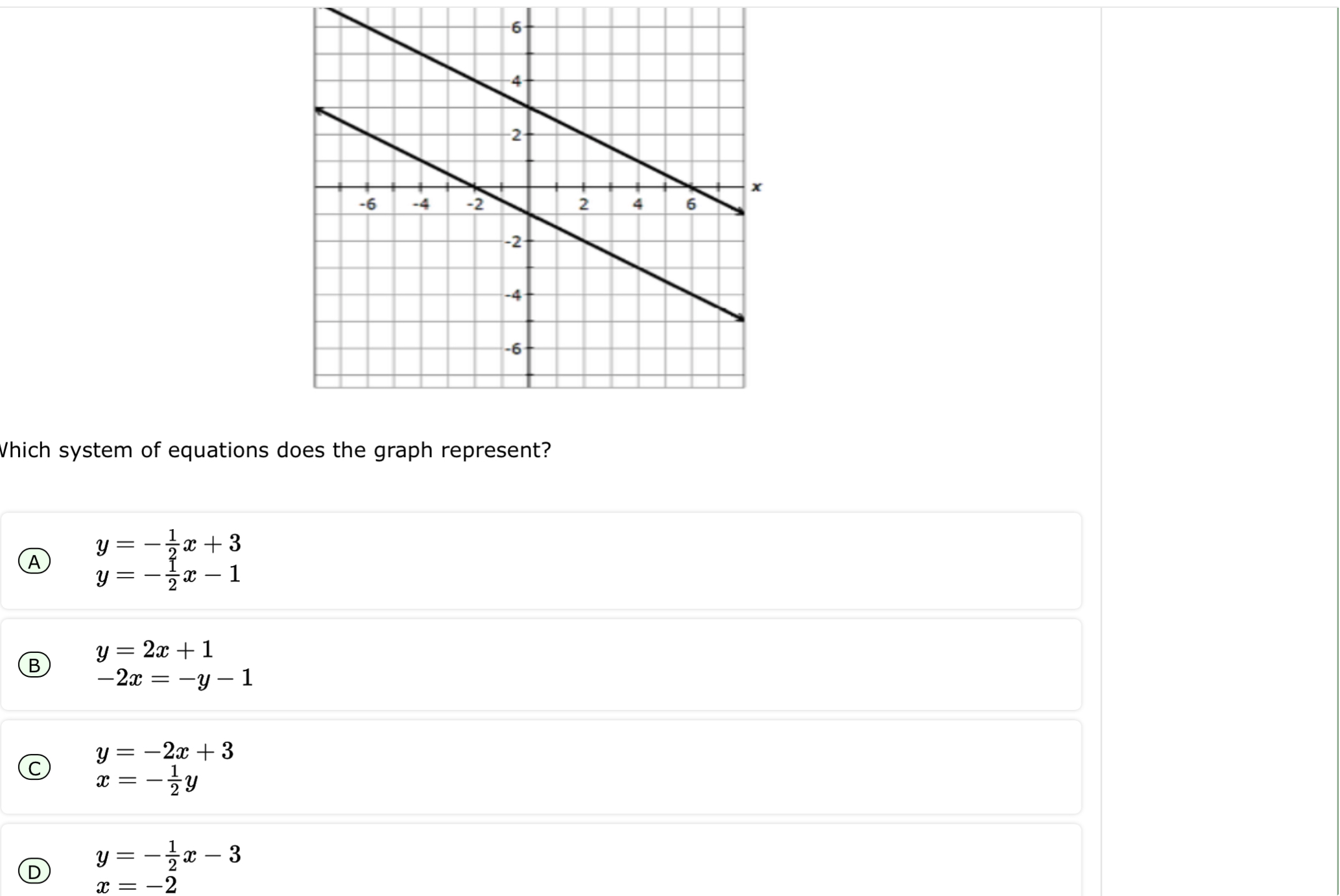
Which system of equations does the graph represent?

Steps to Solve

1. Identify the slope and y-intercept of the first line

   • Observe the first line from the graph. It appears to pass through points such as (0, 3) and (2, 2).
   • The slope ($m_1$) can be calculated as: $$ m_1 = \frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - 3}{2 - 0} = -\frac{1}{2} $$
   • Thus, the equation can be expressed in slope-intercept form as: $$ y = -\frac{1}{2}x + 3 $$

2. Identify the slope and y-intercept of the second line

   • Now, observe the second line. It passes through points like (0, -1) and (2, -2).
   • The slope ($m_2$) can be calculated as: $$ m_2 = \frac{-2 - (-1)}{2 - 0} = -\frac{1}{2} $$
   • Thus, the equation in slope-intercept form becomes: $$ y = -\frac{1}{2}x - 1 $$

3. Compare with answer choices

   • Now, we compare our derived equations with the provided options:
     • Option A: $$ y = -\frac{1}{2}x + 3 $$ $$ y = -\frac{1}{2}x - 1 $$
     • This matches our derived equations from the graph.

4. Evaluate other options for verification

   • Option B: $y = 2x + 1$ and $-2x = -y - 1$ does not produce matching equations for the slope and intercept observed in the graph.
   • Option C and D are similarly mismatched on slopes and intercepts.