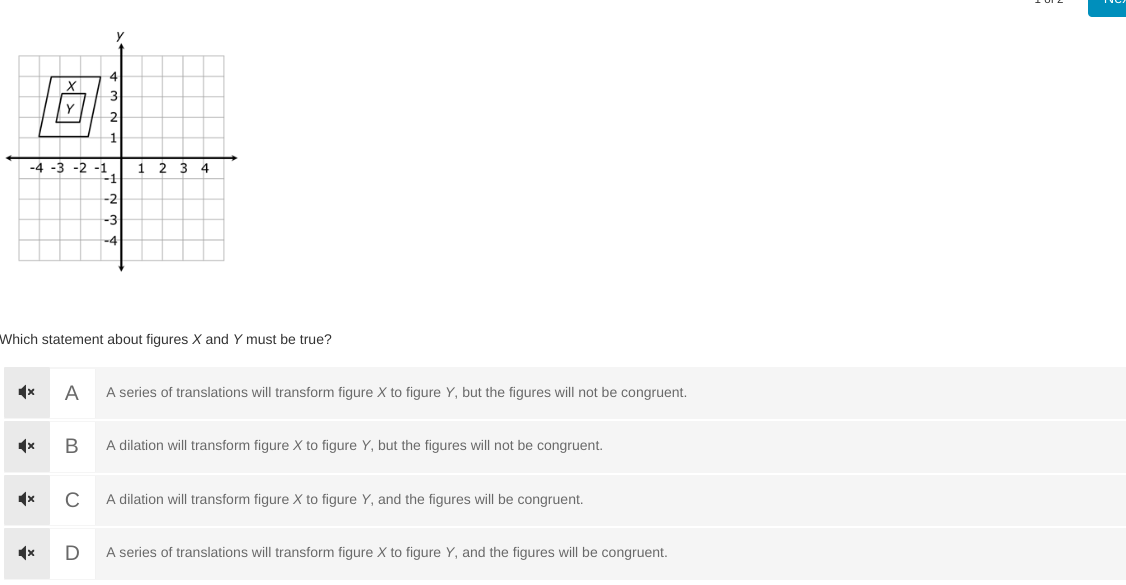
Which statement about figures X and Y must be true?
Understand the Problem
The question is asking which statement regarding transformations between figures X and Y is necessarily true. The options consider the types of transformations (translations or dilations) and their implications for congruence.
Answer
A series of translations will transform figure X to figure Y, but the figures will not be congruent.
Answer for screen readers
A series of translations will transform figure X to figure Y, but the figures will not be congruent.
Steps to Solve
-
Identify the type of figures Both figures X and Y appear to be rectangles, each situated at different positions and sizes on the coordinate plane.
-
Analyze transformations Examine the transformations required to change figure X into figure Y. Transformations can include translations (moving without changing shape or size), dilations (changing size but maintaining shape), and rotations (turning around a point).
-
Evaluate congruence Determine if the figures can be made congruent (same shape and size) through transformations. If a dilation occurs, the figures can become similar but not congruent unless the scale factor is 1 (which is a trivial case).
-
Check each option Assess each statement provided:
- Option A: Translations don’t change size; if the figures have different sizes, they cannot be congruent.
- Option B: Dilation usually changes size, but this statement claims they won't be congruent, which can be true if the scale factor is not 1.
- Option C: This assumes that the figures will be the same size after dilation, which is incorrect based on our observations.
- Option D: If translations are not congruent and they differ in dimensions, this contradicts proximity.
- Conclude based on analysis From the analysis, determine which statement must be true given that translations cannot create congruency if the figures have different sizes.
A series of translations will transform figure X to figure Y, but the figures will not be congruent.
More Information
In geometry, the term "congruent" means that the shapes have the same size and shape. The transformation of a figure through translation does not alter its size and shape, making statement A a necessity.
Tips
- Assuming that all types of transformations can result in congruency without checking the scale or type.
- Misunderstanding the difference between similarity (same shape but different sizes) and congruency (same shape and size).
AI-generated content may contain errors. Please verify critical information