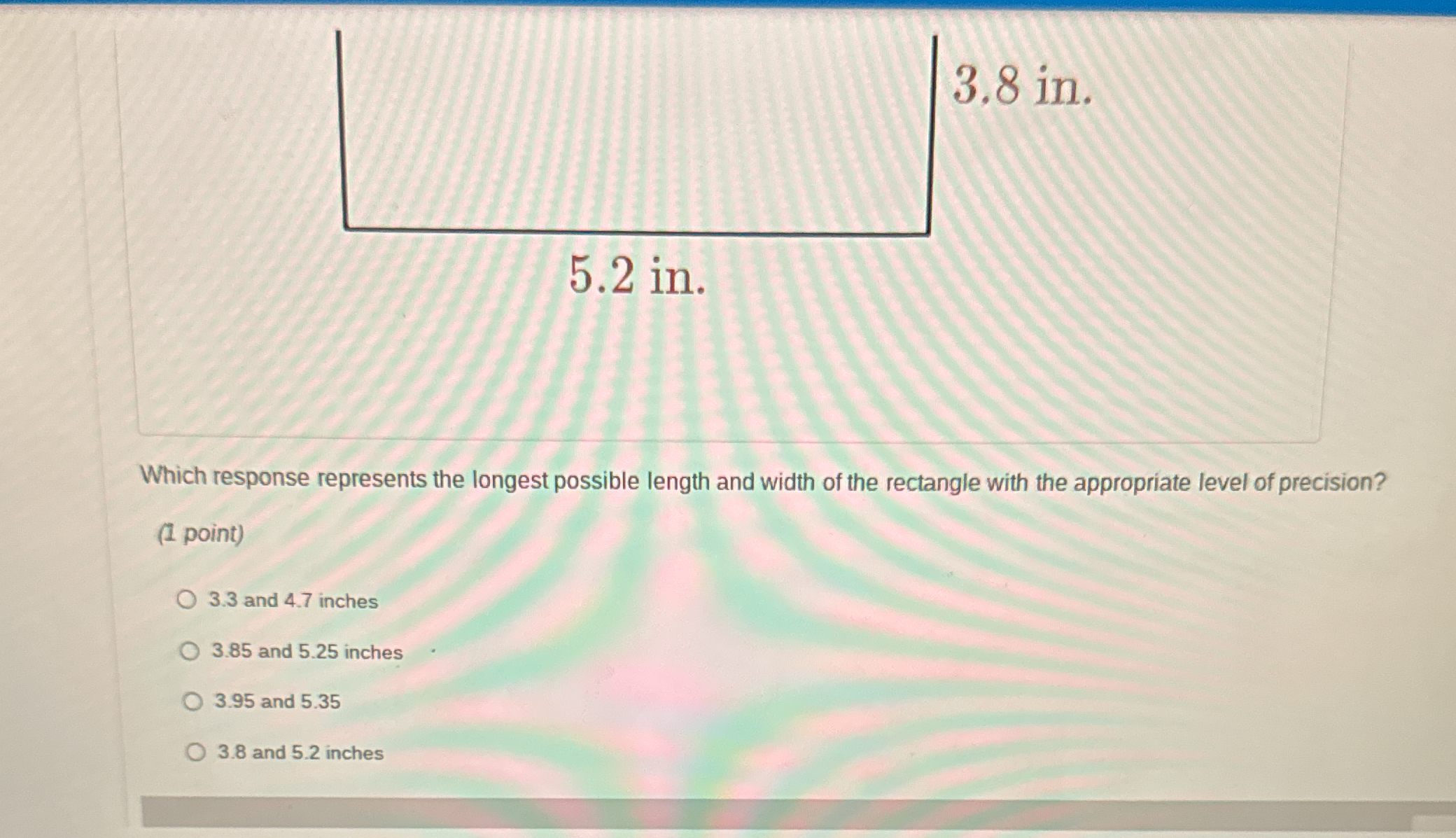
Which response represents the longest possible length and width of the rectangle with the appropriate level of precision?
Understand the Problem
The question is asking for the longest possible length and width of a rectangle based on given dimensions, considering the appropriate level of precision.
Answer
The longest possible dimensions are $3.85$ and $5.25$ inches.
Answer for screen readers
The longest possible length and width of the rectangle with the appropriate level of precision is 3.85 and 5.25 inches.
Steps to Solve
-
Understanding Length and Width
The given dimensions of the rectangle are 5.2 inches and 3.8 inches. We need to find the longest possible dimensions based on these values.
-
Adjusting for Precision
The relevant precision for the dimensions can be determined by looking at the decimal places. The values are both presented to one decimal place (5.2 and 3.8). Thus, any longer value must maintain that level of precision.
-
Calculating Maximum Values
To find the longest possible lengths, we can round the given dimensions to the nearest hundredth:
- For 5.2 inches, the closest maximum value maintaining precision is 5.25 inches.
- For 3.8 inches, the closest maximum value maintaining precision is 3.85 inches.
-
Identifying Correct Option
We then look for options that match the calculated maximum lengths of 5.25 inches and 3.85 inches.
The longest possible length and width of the rectangle with the appropriate level of precision is 3.85 and 5.25 inches.
More Information
In geometry, precision is key, especially when dealing with measurements. The ability to properly round and maintain significant figures is crucial in accurately representing dimensions.
Tips
- Rounding improperly: Ensure that you follow the correct rounding rules based on significant figures.
- Overlooking precision: Always align the precision of the final values with the one provided in the problem.
AI-generated content may contain errors. Please verify critical information