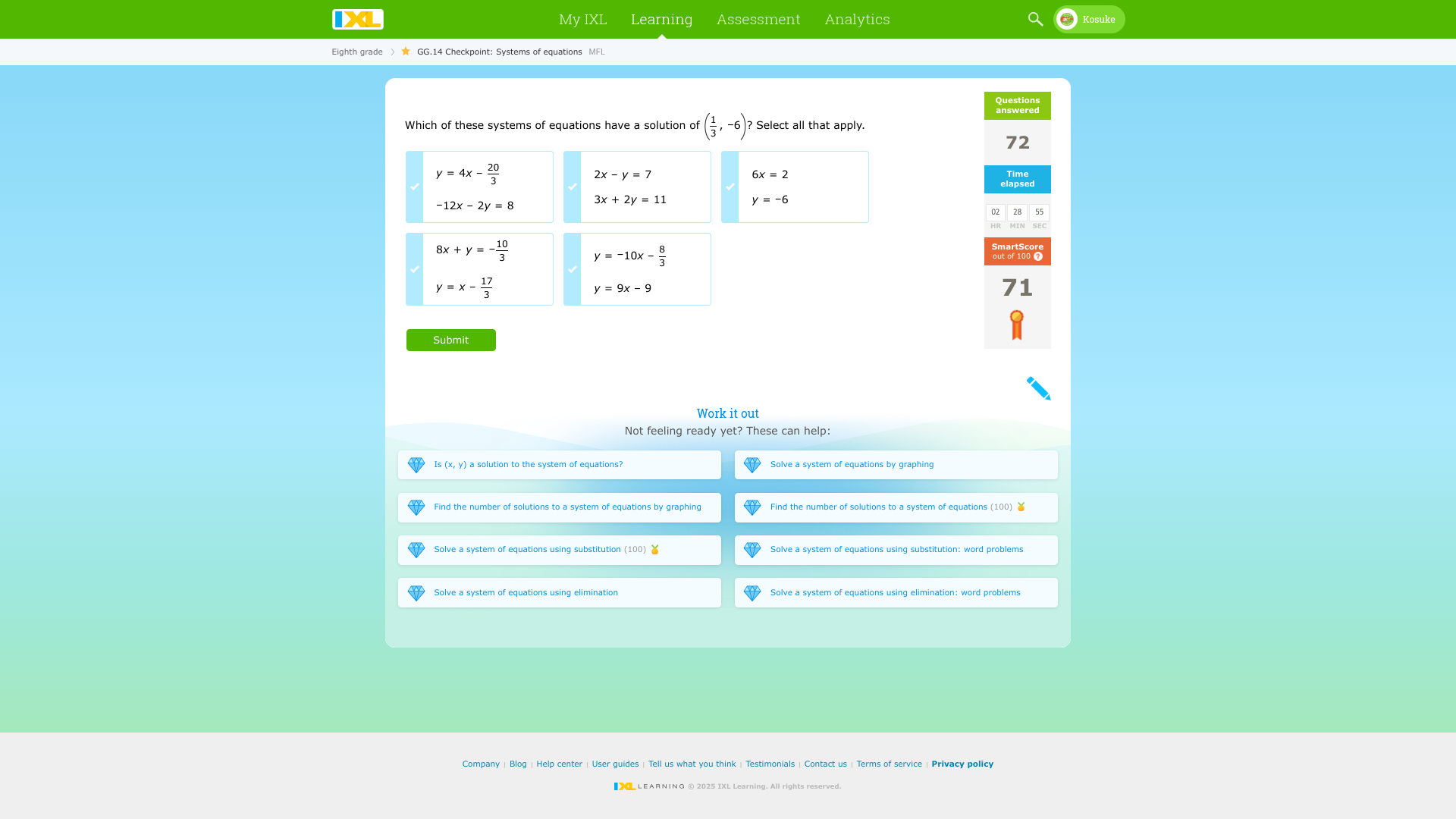
Which of these systems of equations have a solution of (1/3, -6)? Select all that apply.

Steps to Solve

1. Substituting the values into equations First, we can substitute the specific values of (x = \frac{1}{3}) and (y = -6) into each equation to check if they hold true.

2. Evaluate the first equation: For the equation (y = 4x - \frac{20}{3}),

Substituting the values: $$ -6 = 4 \left(\frac{1}{3}\right) - \frac{20}{3} $$ Calculating the right side: $$ -6 = \frac{4}{3} - \frac{20}{3} $$ Which simplifies to: $$ -6 = \frac{4 - 20}{3} $$ $$ -6 = \frac{-16}{3} $$ This is false.

3. Evaluate the second equation: For the equations (2x - y = 7) and (3x + 2y = 11),

Substituting into the first equation: $$ 2\left(\frac{1}{3}\right) - (-6) = 7 $$ $$ \frac{2}{3} + 6 = 7 $$ This simplifies to: $$ \frac{2}{3} + \frac{18}{3} = \frac{20}{3} \quad \text{(not true)} $$

Next, check the second: $$ 3\left(\frac{1}{3}\right) + 2(-6) = 11 $$ $$ 1 - 12 = 11 $$ This is false.

4. Evaluate the third equation: For the equation (8x + y = -\frac{10}{3}),

Substituting: $$ 8\left(\frac{1}{3}\right) + (-6) = -\frac{10}{3} $$ $$ \frac{8}{3} - 6 = -\frac{10}{3} $$ Which is: $$ \frac{8}{3} - \frac{18}{3} = -\frac{10}{3} $$ This is true.

5. Evaluate the fourth equation: For the equations (y = -\frac{10}{3}) and (y = 9x - 9),

Substituting (y): $$ -6 = 9\left(\frac{1}{3}\right) - 9 $$ $$ -6 = 3 - 9 $$ This evaluates to true since: $$ -6 = -6 $$

6. Final evaluation of all systems The valid systems of equations are the ones that yield true results when (x = \frac{1}{3}) and (y = -6).