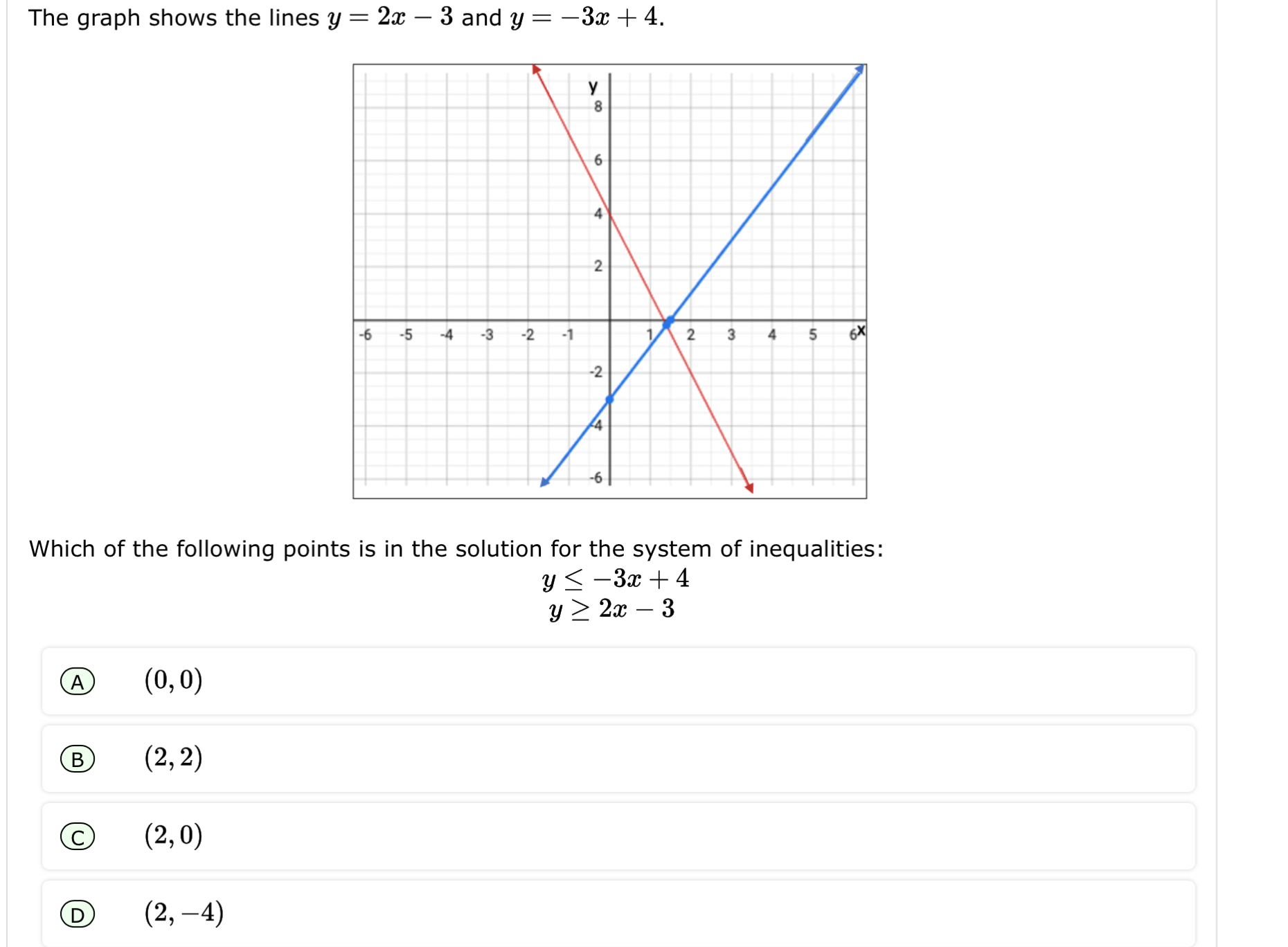
Which of the following points is in the solution for the system of inequalities: y ≤ -3x + 4 and y ≥ 2x - 3?

Steps to Solve

1. Understand the inequalities
   We have the inequalities:
   $$ y \leq -3x + 4 $$
   $$ y \geq 2x - 3 $$
   We need to find which of the given points satisfies both inequalities.

2. Check Point A: (0, 0)
   Substitute ( x = 0 ) and ( y = 0 ) into both inequalities.
   For the first inequality:
   $$ 0 \leq -3(0) + 4 \implies 0 \leq 4 \quad \text{(True)} $$
   For the second inequality:
   $$ 0 \geq 2(0) - 3 \implies 0 \geq -3 \quad \text{(True)} $$

3. Check Point B: (2, 2)
   Substitute ( x = 2 ) and ( y = 2 ) into both inequalities.
   For the first inequality:
   $$ 2 \leq -3(2) + 4 \implies 2 \leq -6 + 4 \implies 2 \leq -2 \quad \text{(False)} $$
   For the second inequality:
   $$ 2 \geq 2(2) - 3 \implies 2 \geq 4 - 3 \implies 2 \geq 1 \quad \text{(True)} $$

4. Check Point C: (2, 0)
   Substitute ( x = 2 ) and ( y = 0 ) into both inequalities.
   For the first inequality:
   $$ 0 \leq -3(2) + 4 \implies 0 \leq -6 + 4 \implies 0 \leq -2 \quad \text{(False)} $$
   For the second inequality:
   $$ 0 \geq 2(2) - 3 \implies 0 \geq 4 - 3 \implies 0 \geq 1 \quad \text{(False)} $$

5. Check Point D: (2, -4)
   Substitute ( x = 2 ) and ( y = -4 ) into both inequalities.
   For the first inequality:
   $$ -4 \leq -3(2) + 4 \implies -4 \leq -6 + 4 \implies -4 \leq -2 \quad \text{(False)} $$
   For the second inequality:
   $$ -4 \geq 2(2) - 3 \implies -4 \geq 4 - 3 \implies -4 \geq 1 \quad \text{(False)} $$

6. Conclusion
   The only point that satisfies both inequalities is Point A: ( (0, 0) ).