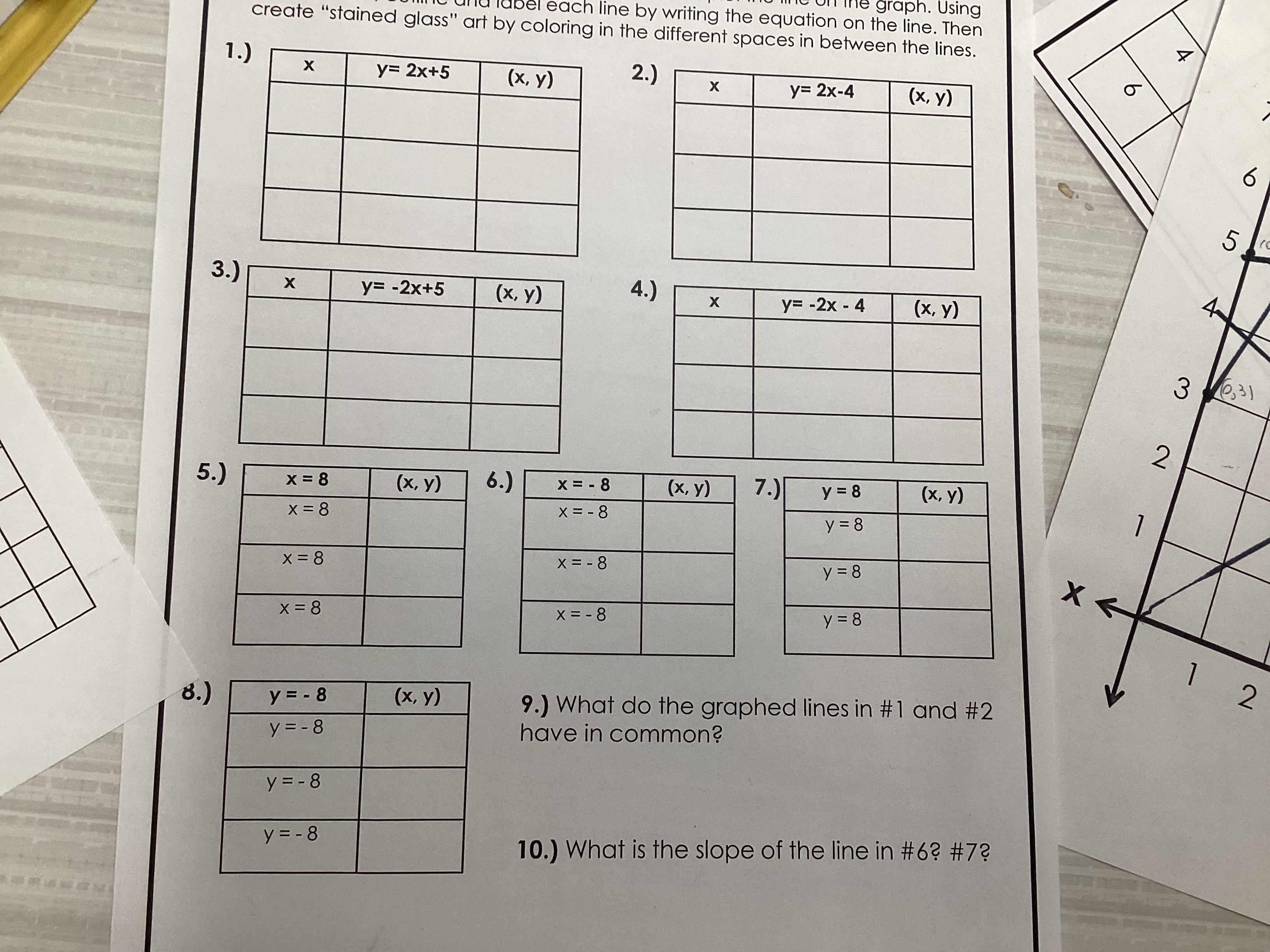
What do the graphed lines in #1 and #2 have in common? What is the slope of the line in #6? #7?

Understand the Problem

The question is about graphing linear equations and analyzing their properties. It asks to create tables of coordinates for given equations, graph them, and then analyze common characteristics and slopes of specific lines.

Answer

1.) $(-2, 1)$, $(-1, 3)$, $(0, 5)$, $(1, 7)$, $(2, 9)$ 2.) $(-2, -8)$, $(-1, -6)$, $(0, -4)$, $(1, -2)$, $(2, 0)$ 3.) $(-2, 9)$, $(-1, 7)$, $(0, 5)$, $(1, 3)$, $(2, 1)$ 4.) $(-2, 0)$, $(-1, -2)$, $(0, -4)$, $(1, -6)$, $(2, -8)$ 5.) Points: $(8, y)$ for various $y$ values. 6.) Points: $(x, -8)$ for various $x$ values. 9.) Different slopes; intersect in one point. 10.) Undefined for #6, $0$ for #7.

Steps to Solve

Finding Coordinates for the First Equation
For the equation $y = 2x + 5$, choose values for $x$ (e.g., $-2, -1, 0, 1, 2$).
Calculate $y$ for each value:

For $x = -2$: $y = 2(-2) + 5 = 1$ → Coordinates: $(-2, 1)$
For $x = -1$: $y = 2(-1) + 5 = 3$ → Coordinates: $(-1, 3)$
For $x = 0$: $y = 2(0) + 5 = 5$ → Coordinates: $(0, 5)$
For $x = 1$: $y = 2(1) + 5 = 7$ → Coordinates: $(1, 7)$
For $x = 2$: $y = 2(2) + 5 = 9$ → Coordinates: $(2, 9)$

Finding Coordinates for the Second Equation
For $y = 2x - 4$, choose the same $x$ values.
Calculate $y$:

For $x = -2$: $y = 2(-2) - 4 = -8$ → Coordinates: $(-2, -8)$
For $x = -1$: $y = 2(-1) - 4 = -6$ → Coordinates: $(-1, -6)$
For $x = 0$: $y = 2(0) - 4 = -4$ → Coordinates: $(0, -4)$
For $x = 1$: $y = 2(1) - 4 = -2$ → Coordinates: $(1, -2)$
For $x = 2$: $y = 2(2) - 4 = 0$ → Coordinates: $(2, 0)$

Finding Coordinates for the Third Equation
For $y = -2x + 5$, choose the same $x$ values.
Calculate $y$:

For $x = -2$: $y = -2(-2) + 5 = 9$ → Coordinates: $(-2, 9)$
For $x = -1$: $y = -2(-1) + 5 = 7$ → Coordinates: $(-1, 7)$
For $x = 0$: $y = -2(0) + 5 = 5$ → Coordinates: $(0, 5)$
For $x = 1$: $y = -2(1) + 5 = 3$ → Coordinates: $(1, 3)$
For $x = 2$: $y = -2(2) + 5 = 1$ → Coordinates: $(2, 1)$

Finding Coordinates for the Fourth Equation
For $y = -2x - 4$, perform the same steps:

For $x = -2$: $y = -2(-2) - 4 = 0$ → Coordinates: $(-2, 0)$
For $x = -1$: $y = -2(-1) - 4 = -2$ → Coordinates: $(-1, -2)$
For $x = 0$: $y = -2(0) - 4 = -4$ → Coordinates: $(0, -4)$
For $x = 1$: $y = -2(1) - 4 = -6$ → Coordinates: $(1, -6)$
For $x = 2$: $y = -2(2) - 4 = -8$ → Coordinates: $(2, -8)$

Finding Coordinates for the Vertical Line
For the line $x = 8$, all $y$ values can be chosen freely. Use values:

$(-, 1)$, $(-, 2)$, $(-, 3)$, $(-, 4)$ and so on.

Finding Coordinates for the Horizontal Line
For the line $y = -8$, use a similar method:

$(1, -8)$, $(2, -8)$, $(3, -8)$, $(4, -8)$ and so on.

Analyzing Common Properties
For #9, the lines in #1 and #2:
Both are linear equations and have different slopes.
Identify their characteristics, such as direction and intersections.
Finding Slopes
For #10:
To find the slope of line #6 ($x=8$), it is undefined because it's a vertical line.
For line #7, $y=8$, the slope is $0$ because it is horizontal.

1.) Coordinates: $(-2, 1)$, $(-1, 3)$, $(0, 5)$, $(1, 7)$, $(2, 9)$

2.) Coordinates: $(-2, -8)$, $(-1, -6)$, $(0, -4)$, $(1, -2)$, $(2, 0)$

3.) Coordinates: $(-2, 9)$, $(-1, 7)$, $(0, 5)$, $(1, 3)$, $(2, 1)$

4.) Coordinates: $(-2, 0)$, $(-1, -2)$, $(0, -4)$, $(1, -6)$, $(2, -8)$

5.) Points can be: $(8, 1)$, $(8, 2)$, $(8, 3)$, $(8, 4)$, etc.

6.) Points can be: $(1, -8)$, $(2, -8)$, $(3, -8)$, $(4, -8)$, etc.

9.) Both lines have different slopes; they intersect at one point.

10.) The slope of line #6 is undefined; the slope of line #7 is $0$.

More Information

These equations represent various linear functions. In a graph, linear functions appear as straight lines. A vertical line has an undefined slope, while a horizontal line has a slope of 0. Understanding these concepts is crucial for graphing and analyzing equations.

Tips

Confusing the slope of vertical and horizontal lines.
Not choosing a sufficient range of $x$ values for complete coordinate tables.
Forgetting to check for intersections between lines.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!