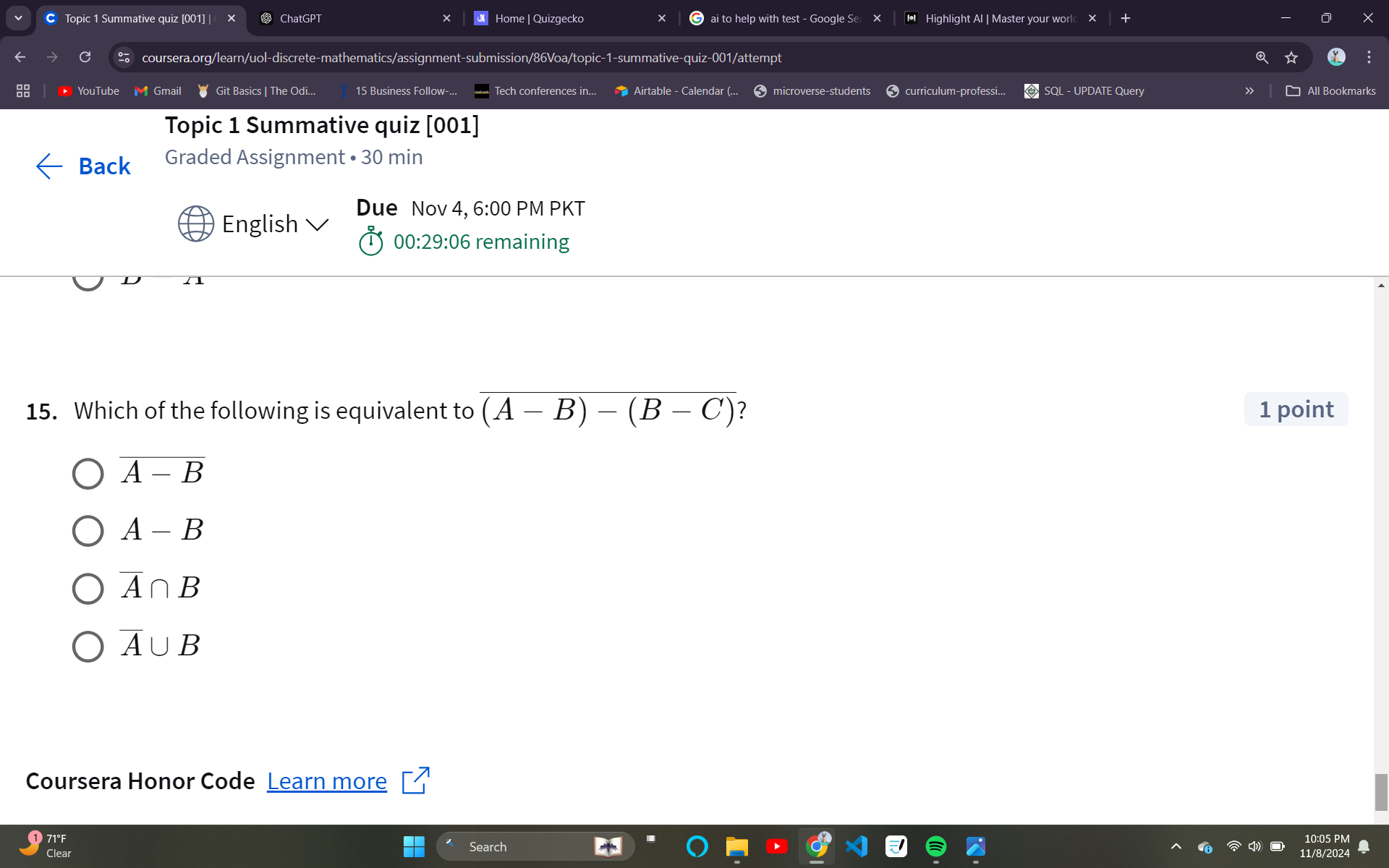
Which of the following is equivalent to (A - B) - (B - C)?

Steps to Solve

1. Apply De Morgan's Laws We start with the expression ( \overline{(A - B)} - \overline{(B - C)} ). According to De Morgan’s laws, we can rewrite the complements: $$ \overline{(A - B)} = \overline{A} \cup B $$ $$ \overline{(B - C)} = \overline{B} \cup C $$

2. Substitute De Morgan's Results Now, substitute the results from the first step into the original expression: $$ \overline{(A - B)} - \overline{(B - C)} = (\overline{A} \cup B) - (\overline{B} \cup C) $$

3. Rewrite the Resulting Expression To simplify this expression, we need to recognize that subtracting a union means we need to consider the intersection: $$ (X - Y) = X \cap \overline{Y} $$ So we can rewrite: $$ (\overline{A} \cup B) \cap \overline{(\overline{B} \cup C)} $$

4. Simplify Further Now, applying De Morgan’s laws again to simplify the negation: $$ \overline{(\overline{B} \cup C)} = B \cap \overline{C} $$

So the expression becomes: $$ (\overline{A} \cup B) \cap (B \cap \overline{C}) $$

5. Distribute and Combine Now distribute: $$ (\overline{A} \cap B \cap \overline{C}) \cup (B \cap B \cap \overline{C}) $$ This simplifies to: $$ (B \cap \overline{C}) \cup (\overline{A} \cap B) $$

So the final expression can be rewritten as: $$ B \cap (\overline{C} \cup \overline{A}) $$