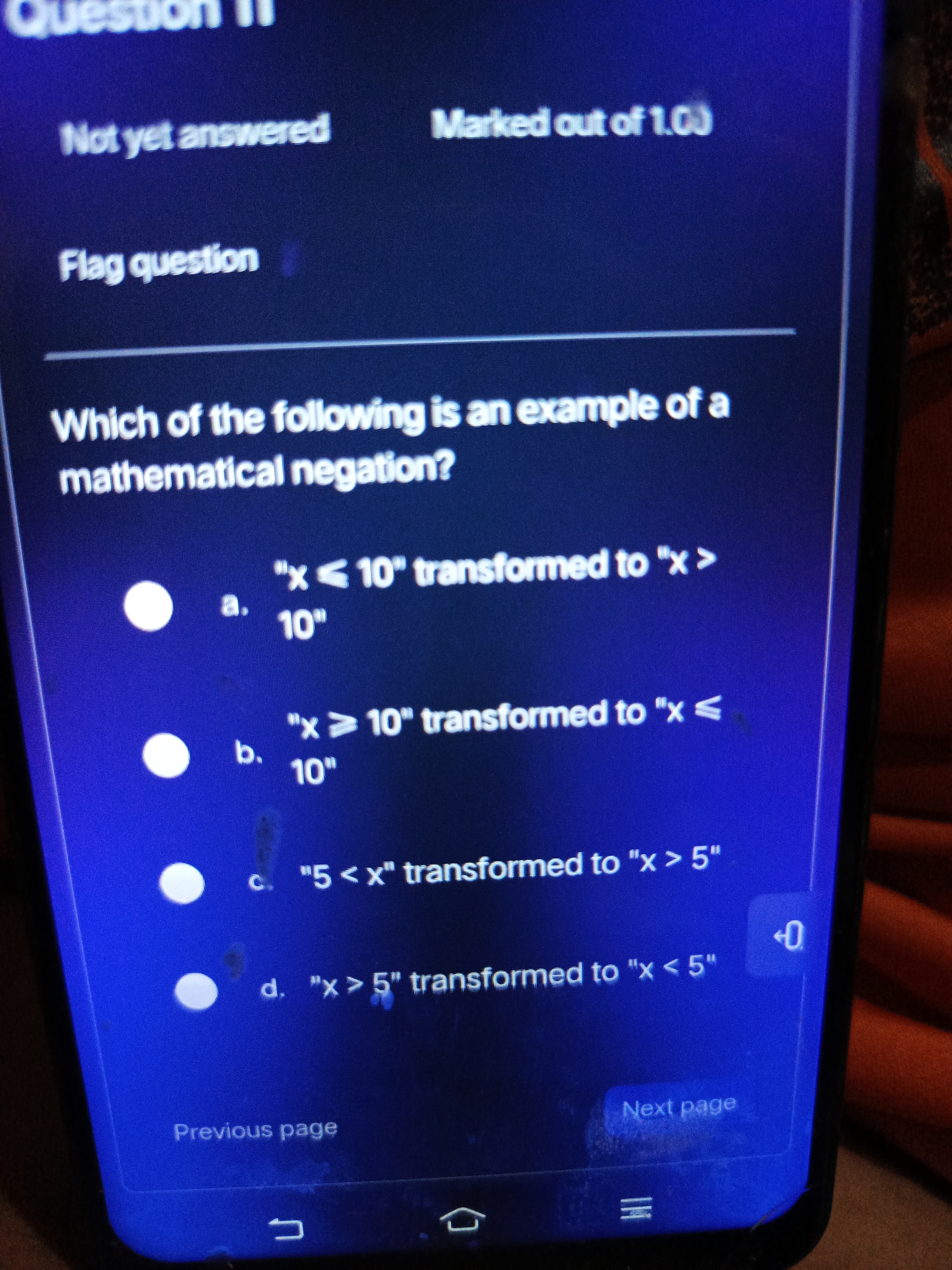
Which of the following is an example of a mathematical negation?
Understand the Problem
The question asks about identifying an example of mathematical negation from the provided options. It focuses on how inequalities can be negated.
Answer
The correct answer is option a: "$x \leq 10$" transformed to "$x > 10$".
Answer for screen readers
The correct answer is option a: "$x \leq 10$" transformed to "$x > 10$".
Steps to Solve
-
Understanding Mathematical Negation Mathematical negation involves reversing the true/false value of a statement. For inequalities, this means changing the inequality sign.
-
Examining the Options
- Option a: "$x \leq 10$" transformed to "$x > 10$". This is the negation; if $x$ is not less than or equal to 10, it must be greater than 10.
- Option b: "$x \geq 10$" transformed to "$x \leq 10$". This is not correct; the negation should be $x < 10$.
- Option c: "$5 < x$" transformed to "$x > 5$". This is not correct; the negation should be $x \leq 5$.
- Option d: "$x > 5$" transformed to "$x < 5$". This is incorrect as well; the negation would be $x \leq 5$.
-
Identifying the Correct Option From the analysis, option a is the only example of a correct mathematical negation.
The correct answer is option a: "$x \leq 10$" transformed to "$x > 10$".
More Information
Mathematical negation is essential in logic and algebra, particularly when solving inequalities or making arguments in mathematics. Each inequality has a specific negation that flips its meaning.
Tips
Common mistakes include:
- Confusing greater than/less than signs when negating inequalities.
- Not realizing that the negation must cover all possible outcomes, not just the direct opposite.
AI-generated content may contain errors. Please verify critical information