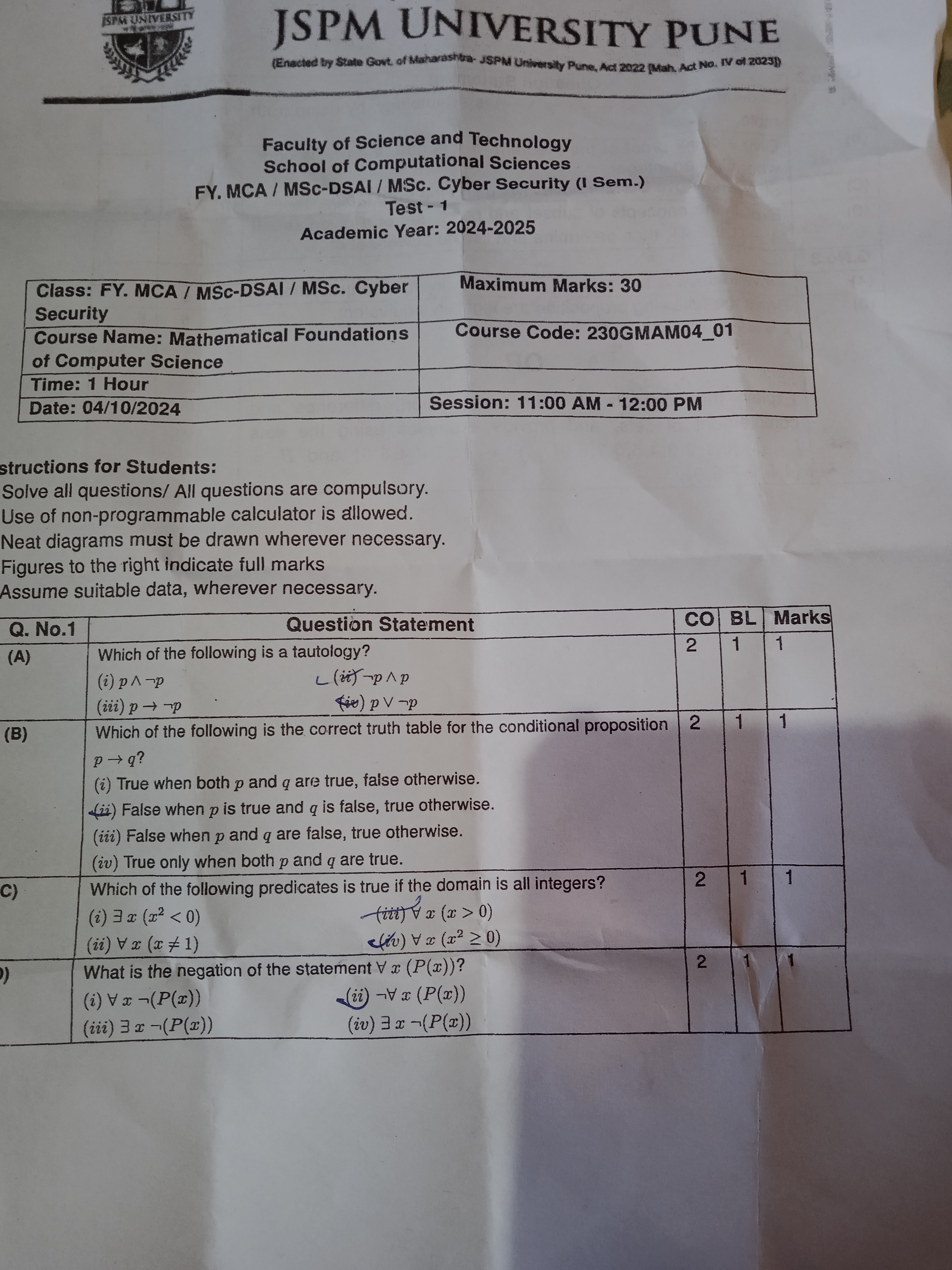
Which of the following is a tautology? Which of the following is the correct truth table for the conditional proposition p → q? Which of the following predicates is true if the dom... Which of the following is a tautology? Which of the following is the correct truth table for the conditional proposition p → q? Which of the following predicates is true if the domain is all integers? What is the negation of the statement ∀x (P(x))?
Understand the Problem
The question provides a test paper with various problems related to mathematical logic, including tautologies, truth tables, predicates, and negation of statements. Each question requires evaluation of logical statements and understanding of their properties.
Answer
1. (i) $p \land \neg p$ 2. (iv) True only when both $p$ and $q$ are true. 3. (iii) $\exists x (x > 0)$ and (iv) $\forall x (x \geq 0)$. 4. (ii) $\exists x (\neg P(x))$.
Answer for screen readers
- The tautology is (i) $p \land \neg p$.
- The correct truth table for $p \to q$ is (iv) True only when both $p$ and $q$ are true.
- The true predicates are (iii) $\exists x (x > 0)$ and (iv) $\forall x (x \geq 0)$.
- The correct negation of $\forall x (P(x))$ is (ii) $\exists x (\neg P(x))$.
Steps to Solve
-
Identify the tautology
A tautology is a logical statement that is always true, regardless of the truth values of its components. We evaluate each option to determine which one holds true under all circumstances. -
Evaluate truth tables
For the conditional proposition $p \to q$, construct a truth table. The table should list combinations of true and false values for $p$ and $q$, and check the truth value of the proposition. -
Verify predicates
For each predicate based on the domain of all integers, assess the truth of the given statements, like whether $\exists x (x < 0)$ is true when considering all integers. -
Negate the statement
To negate the statement $\forall x (P(x))$, apply the concept of negation, which converts universal quantifiers to existential quantifiers. Use De Morgan's laws to correctly form the negation.
- The tautology is (i) $p \land \neg p$.
- The correct truth table for $p \to q$ is (iv) True only when both $p$ and $q$ are true.
- The true predicates are (iii) $\exists x (x > 0)$ and (iv) $\forall x (x \geq 0)$.
- The correct negation of $\forall x (P(x))$ is (ii) $\exists x (\neg P(x))$.
More Information
- A tautology exemplifies logical consistency in propositions.
- Truth tables are essential tools in logical reasoning for determining the validity of arguments.
- Predicates must be interpreted accurately based on their domains to avoid misidentifying their truth values.
Tips
- Confusing a tautology with other logical statements. Always test with different truth values.
- Misconstructing the truth table; ensure all combinations are covered accurately.
- Negating statements incorrectly; remember that negating a universal quantifier requires switching to an existential quantifier and vice versa.
AI-generated content may contain errors. Please verify critical information