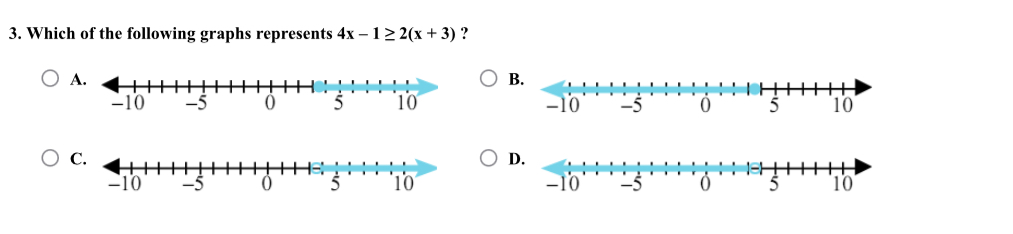
Which of the following graphs represents 4x - 1 ≥ 2(x + 3)?
Understand the Problem
The question asks which of the offered graphs correctly represents the inequality 4x – 1 ≥ 2(x + 3). To solve it, we will first simplify the inequality and then determine its solution set, which will allow us to identify the correct graph.
Answer
The correct graph is the one showing $x \geq 3.5$.
Answer for screen readers
The correct graph represents the inequality is the one that shows $x \geq 3.5$, which is a closed dot at 3.5 and an arrow extending to the right.
Steps to Solve
- Simplify the Inequality
We start with the inequality:
$$ 4x - 1 \geq 2(x + 3) $$
Expanding the right side gives:
$$ 4x - 1 \geq 2x + 6 $$
- Isolate x
Next, we isolate $x$ on one side by subtracting $2x$ from both sides:
$$ 4x - 2x - 1 \geq 6 $$
This simplifies to:
$$ 2x - 1 \geq 6 $$
- Add 1 to Both Sides
Now we add 1 to both sides of the inequality:
$$ 2x \geq 7 $$
- Divide by 2
Finally, divide both sides by 2 to find $x$:
$$ x \geq \frac{7}{2} $$
Which simplifies to:
$$ x \geq 3.5 $$
- Identify the Solution Set
The solution set indicates that $x$ includes all numbers greater than or equal to 3.5. Thus, we represent this on a number line:
- A closed dot at 3.5 and an arrow extending to the right.
The correct graph represents the inequality is the one that shows $x \geq 3.5$, which is a closed dot at 3.5 and an arrow extending to the right.
More Information
The inequality tells us that any number greater than or equal to 3.5 satisfies the condition. This is significant because it shows how inequalities can represent a range of solutions rather than just a single value.
Tips
- Misinterpreting the inequality direction: Remember that if the inequality is "greater than or equal to" (≥), then you include the value at the boundary (closed dot).
- Failing to correctly isolate $x$: Ensure each step maintains the inequality's direction and is simplified properly.
AI-generated content may contain errors. Please verify critical information