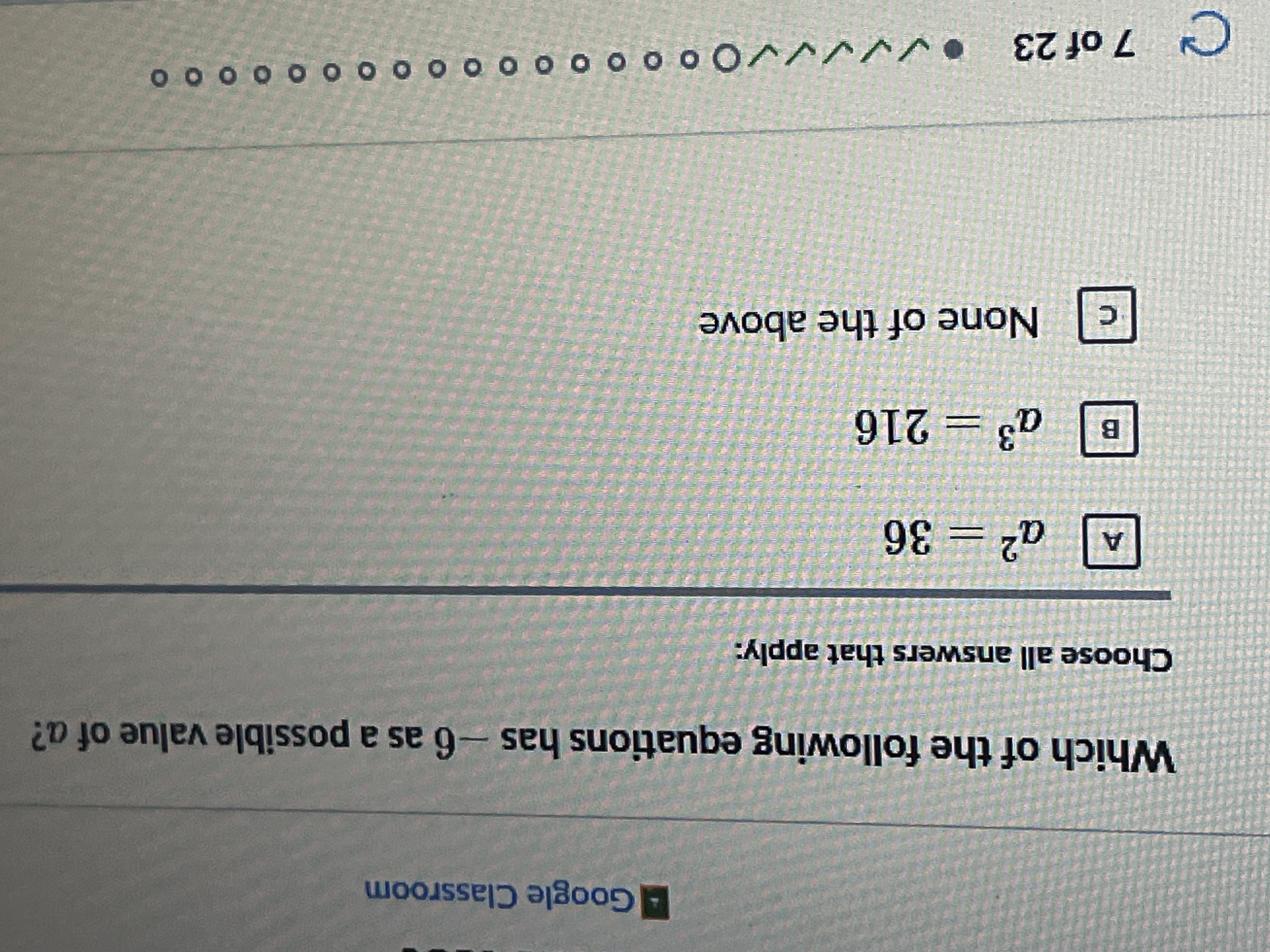
Which of the following equations has -6 as a possible value of a? Choose all answers that apply:
Understand the Problem
The question is asking which equations can have -6 as a possible value for the variable a. We need to evaluate the provided equations to determine if they allow for -6 as a solution.
Answer
A
Answer for screen readers
The answer is A.
Steps to Solve
- Evaluate equation A: ( a^2 = 36 )
To find the possible values of ( a ), take the square root of both sides:
$$ a = \pm \sqrt{36} $$
This simplifies to:
$$ a = 6 \quad \text{or} \quad a = -6 $$
So, ( -6 ) is a possible solution for this equation.
- Evaluate equation B: ( a^3 = 216 )
To find the value of ( a ), take the cube root of both sides:
$$ a = \sqrt[3]{216} $$
Calculating the cube root:
$$ a = 6 $$
Since cube roots yield only one real value, ( -6 ) is not a solution for this equation.
- Conclusion
Based on the evaluations:
- Equation A allows ( a = -6 ).
- Equation B only allows ( a = 6 ).
- Therefore, select all that apply.
The answer is A.
More Information
Equation ( a^2 = 36 ) has both positive and negative solutions, while equation ( a^3 = 216 ) has only the positive solution. Thus, the only equation that supports ( a = -6 ) is equation A.
Tips
- Ignoring negative roots: Many forget that squaring a number can yield both positive and negative values.
- Confusing square roots with cube roots: It's crucial to remember that cube roots only provide one real solution.
AI-generated content may contain errors. Please verify critical information