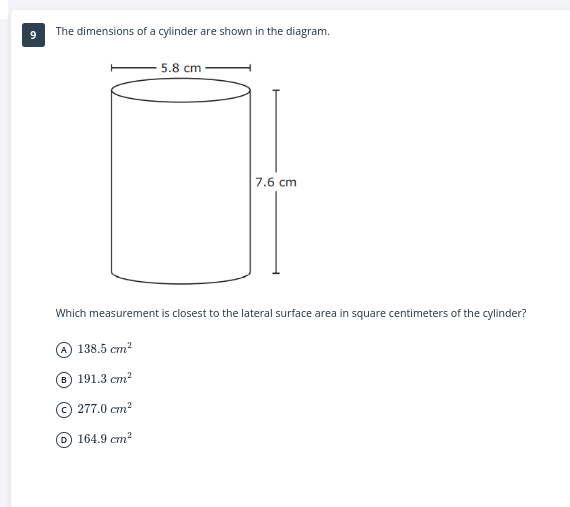
Which measurement is closest to the lateral surface area in square centimeters of the cylinder?

Steps to Solve

1. Identify the dimensions of the cylinder

The height ($h$) is given as $7.6 , \text{cm}$ and the diameter ($d$) is given as $5.8 , \text{cm}$.

2. Calculate the radius of the cylinder

The radius ($r$) can be calculated by dividing the diameter by $2$:

$$ r = \frac{d}{2} = \frac{5.8 , \text{cm}}{2} = 2.9 , \text{cm} $$

3. Use the formula for the lateral surface area of a cylinder

The formula for the lateral surface area ($A$) is:

$$ A = 2 \pi r h $$

Substituting the known values for $r$ and $h$:

$$ A = 2 \pi (2.9 , \text{cm})(7.6 , \text{cm}) $$

4. Calculate the lateral surface area

Now we can calculate the lateral surface area:

1. First, calculate the product of the radius and the height:

$$ 2.9 \times 7.6 = 22.04 , \text{cm}^2 $$

2. Next, multiply by $2\pi$:

$$ A \approx 2 \times 3.14 \times 22.04 , \text{cm}^2 $$ $$ A \approx 138.56 , \text{cm}^2 $$

5. Round the result

The lateral surface area is approximately $138.56 , \text{cm}^2$. Rounding this gives us $138.5 , \text{cm}^2$.