Which inequality best represents the range of the function?
Understand the Problem
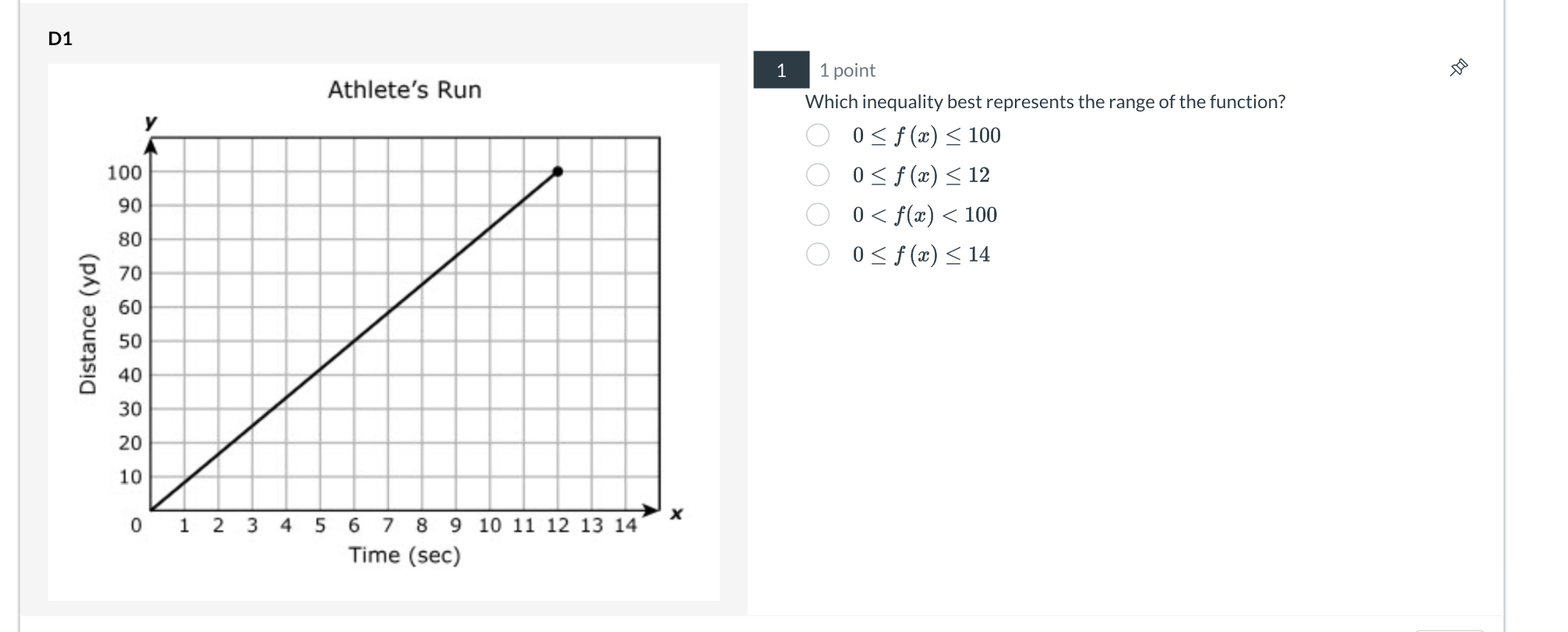
The question is asking which inequality best represents the range of a function based on a provided graph, which displays an athlete's run measured in distance over time.
Answer
$0 \leq f(x) \leq 100$
Answer for screen readers
The correct inequality is $0 \leq f(x) \leq 100$.
Steps to Solve
-
Observe the Graph Examine the graph to determine the maximum and minimum distances traveled by the athlete. The x-axis represents time (in seconds), while the y-axis represents distance (in yards).
-
Identify Maximum Distance From the graph, observe that the athlete reaches a maximum distance of 100 yards when the time is approximately 14 seconds.
-
Determine Minimum Distance The minimum distance starts from the origin (0, 0), indicating that the distance cannot be negative. Therefore, the minimum distance is 0 yards.
-
Formulate the Inequality Based on the observations, the function's range can be expressed as: $$ 0 \leq f(x) \leq 100 $$
-
Select the Correct Option Review the available choices and select the one matching the derived inequality.
The correct inequality is $0 \leq f(x) \leq 100$.
More Information
This inequality indicates that the function representing the athlete's run has a range starting from 0 yards (at the beginning of the run) to a maximum of 100 yards.
Tips
- Ignoring the Graph's Scale: Make sure to correctly interpret the axes and their units.
- Misreading Maximum Values: Double-check the highest point reached on the graph to avoid underestimating the maximum distance.
