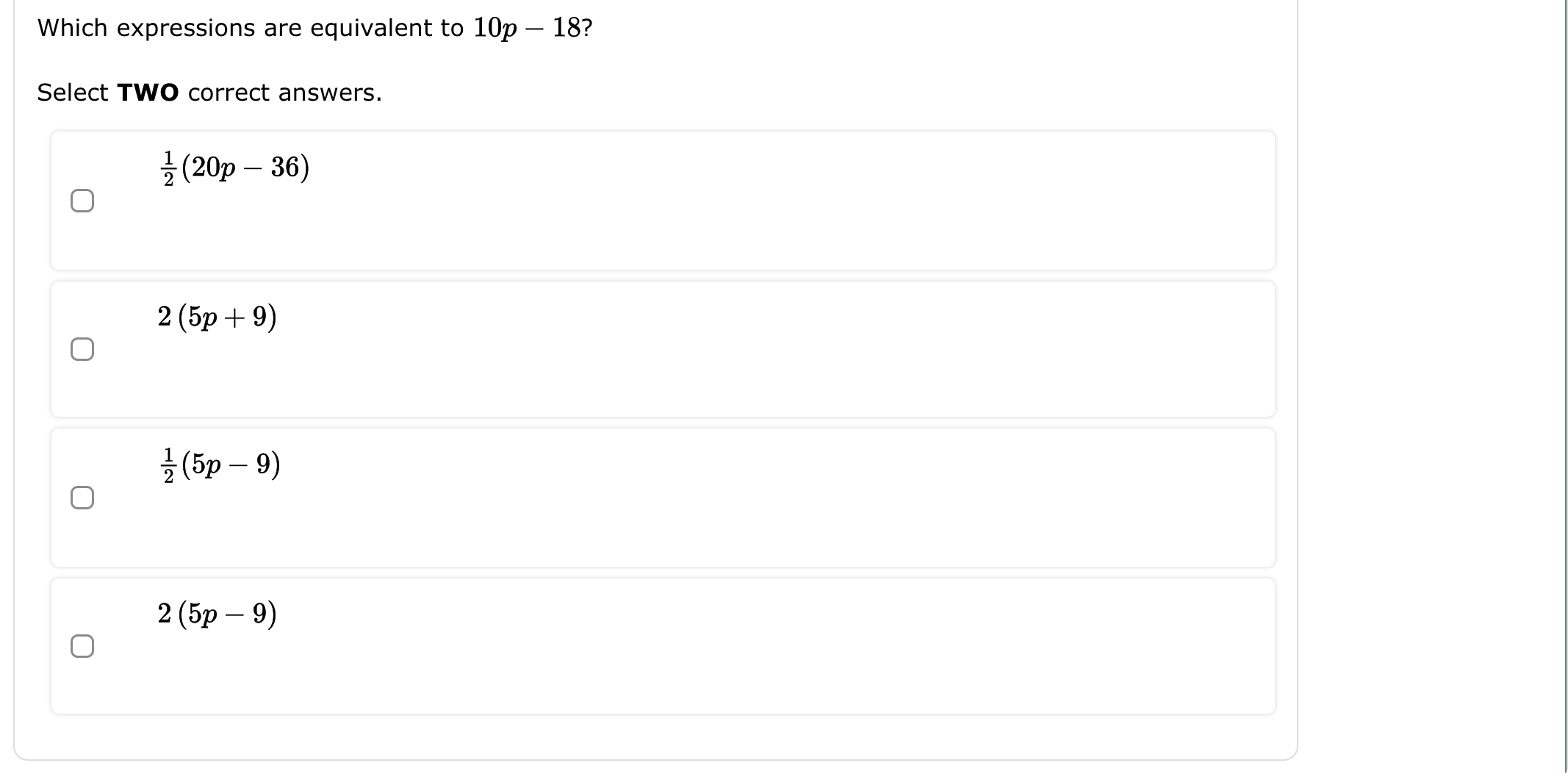
Which expressions are equivalent to 10p - 18? Select TWO correct answers.

Understand the Problem

The question is asking which expressions are equivalent to the expression 10p - 18. The goal is to select two correct answers from the given options based on algebraic manipulation.

Answer

$\frac{1}{2}(20p - 36)$ and $2(5p - 9)$

Steps to Solve

Identify the Target Expression We are looking for expressions that are equivalent to $10p - 18$.
Simplify Each Option We'll simplify each given expression to check for equivalence.
- Option 1: $\frac{1}{2}(20p - 36)$
  - Distributing $\frac{1}{2}$: $$ \frac{1}{2} \cdot 20p - \frac{1}{2} \cdot 36 = 10p - 18 $$
  - This matches our target expression.
- Option 2: $2(5p + 9)$
  - Distributing $2$: $$ 2 \cdot 5p + 2 \cdot 9 = 10p + 18 $$
  - This does not match our target expression.
- Option 3: $\frac{1}{2}(5p - 9)$
  - Distributing $\frac{1}{2}$: $$ \frac{1}{2} \cdot 5p - \frac{1}{2} \cdot 9 = \frac{5p}{2} - \frac{9}{2} $$
  - This does not match our target expression.
- Option 4: $2(5p - 9)$
  - Distributing $2$: $$ 2 \cdot 5p - 2 \cdot 9 = 10p - 18 $$
  - This matches our target expression.
- Option 5: $2(5p)$
  - Distributing $2$: $$ 2 \cdot 5p - 2 \cdot 9 = 10p - 18 $$
  - This matches our target expression.
Conclusion of Options The two expressions equivalent to $10p - 18$ are:

Option 1: $\frac{1}{2}(20p - 36)$
Option 4: $2(5p - 9)$

The two expressions equivalent to $10p - 18$ are:

$\frac{1}{2}(20p - 36)$
$2(5p - 9)$

More Information

Both selected expressions simplify to the same original expression by correctly applying the distributive property. This demonstrates the concept of expression equivalence through algebraic manipulation.

Tips

Confusing the signs when distributing, particularly with negatives (e.g., turning $-9$ into $+9$).
Failing to simplify correctly, especially if not fully applying the distribution step.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!