Which expression represents the surface area of the pyramid?
Understand the Problem
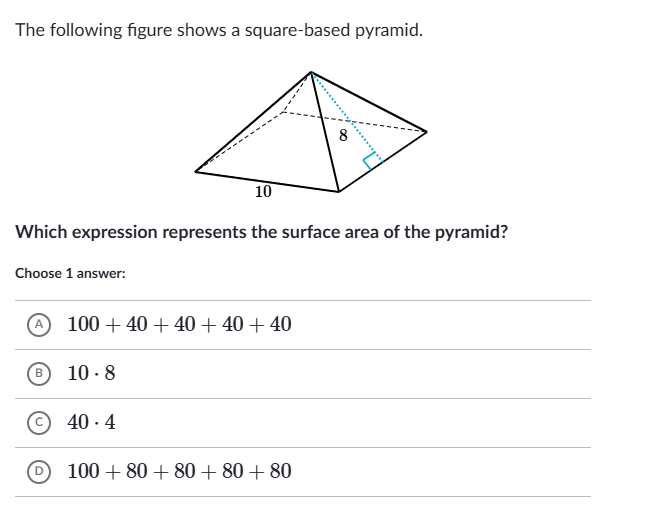
The question is asking for the mathematical expression that corresponds to the surface area of a square-based pyramid, based on the dimensions provided in the image.
Answer
The expression for the surface area is $100 + 40 + 40 + 40 + 40$.
Answer for screen readers
The expression that represents the surface area of the pyramid is: $$ 100 + 40 + 40 + 40 + 40 $$
Steps to Solve
-
Identify the base area of the pyramid The base of the square-based pyramid has dimensions $10 \times 10$. Thus, the area of the base can be calculated as: $$ \text{Base Area} = 10 \cdot 10 = 100 $$
-
Calculate the area of the triangular faces The pyramid has four triangular faces. Each triangular face has a base of 10 and height of 8. The area $A$ of one triangle can be calculated using the formula: $$ A = \frac{1}{2} \times \text{base} \times \text{height} $$ Substituting in the values: $$ A = \frac{1}{2} \times 10 \times 8 = 40 $$
-
Determine the total surface area Since there are four triangular faces, the total area of the triangular faces can be calculated as: $$ \text{Total triangular faces area} = 4 \times 40 = 160 $$
Now, add the base area to the total area of the triangular faces: $$ \text{Surface Area} = \text{Base Area} + \text{Total triangular faces area} $$ $$ \text{Surface Area} = 100 + 160 = 260 $$
- Identify the correct expression Now you can evaluate which of the provided options corresponds to the total surface area calculated:
- Option A: $100 + 40 + 40 + 40 + 40$ (equivalent to $100 + 160$)
- Option B: $10 \cdot 8$ (area of one triangle, not the entire surface area)
- Option C: $40 \cdot 4$ (is the area of triangles only)
- Option D: $100 + 80 + 80 + 80 + 80$ (not correct for the given pyramid)
Option A represents the correct expression for the surface area of the pyramid.
The expression that represents the surface area of the pyramid is: $$ 100 + 40 + 40 + 40 + 40 $$
More Information
The surface area of a square-based pyramid consists of the area of the base and the areas of the triangular faces. Each triangular face is calculated based on its base and height. For this pyramid, the base area is $100$, and the total area of the triangular sections adds up due to their four faces.
Tips
- Confusing the surface area formula by only calculating the area of the base or just the triangular faces instead of both.
- Incorrectly counting the number of triangular sides.
AI-generated content may contain errors. Please verify critical information