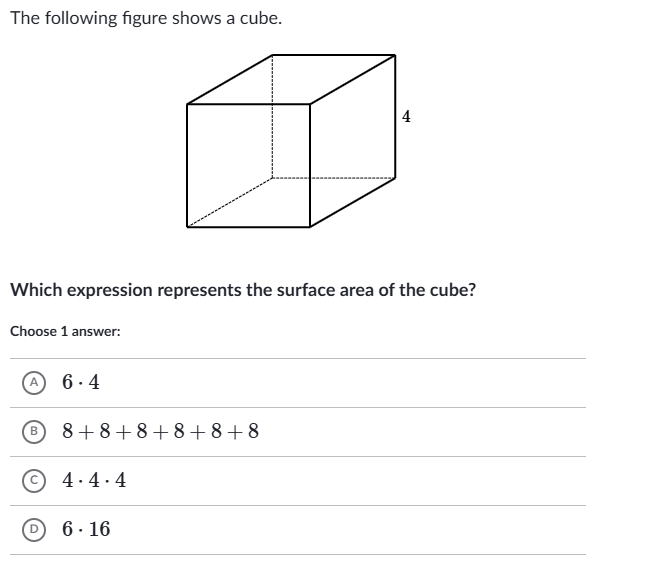
Which expression represents the surface area of the cube?
Understand the Problem
The question is asking which mathematical expression accurately represents the surface area of a cube measuring 4 units on each side. The surface area of a cube can be calculated using the formula 6s², where s is the length of a side.
Answer
The expression representing the surface area of the cube is \( 6 \cdot 16 \).
Answer for screen readers
The surface area of the cube is represented by the expression ( 6 \cdot 16 ), which simplifies to 96.
Steps to Solve
-
Identify the formula for surface area The surface area ( A ) of a cube with side length ( s ) is calculated using the formula: $$ A = 6s^2 $$
-
Substitute the side length into the formula Given that the side length ( s ) is 4 units, we substitute this value into the formula: $$ A = 6(4^2) $$
-
Calculate ( 4^2 ) First, we calculate ( 4^2 ): $$ 4^2 = 16 $$
-
Multiply to find the surface area Now we substitute 16 back into the formula: $$ A = 6 \times 16 $$
-
Calculate the final surface area Finally, we perform the multiplication: $$ A = 96 $$
The surface area of the cube is represented by the expression ( 6 \cdot 16 ), which simplifies to 96.
More Information
The surface area of a cube is always a function of the square of its side length, multiplied by 6, because a cube has 6 identical square faces.
Tips
- Misunderstanding the formula and forgetting to multiply by 6, which leads to only calculating one face's area.
- Confusing the calculation of surface area with volume calculations.
AI-generated content may contain errors. Please verify critical information