Which expression is equivalent to (13x² - 2 + 3x) + (5x - 3x²)?
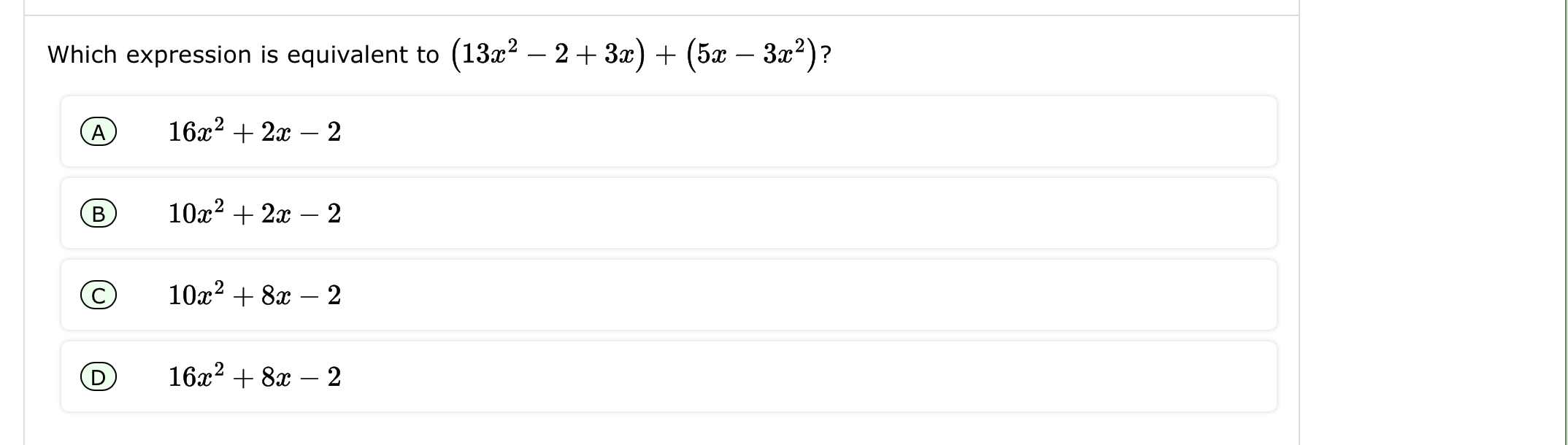
Understand the Problem
The question is asking to simplify the expression (13x² - 2 + 3x) + (5x - 3x²) and identify which of the given options matches the simplified expression. This involves combining like terms and performing basic addition.
Answer
$10x^2 + 8x - 2$
Answer for screen readers
The simplified expression is $10x^2 + 8x - 2$.
Steps to Solve
-
Combine the expressions
Start with the two expressions: $(13x^2 - 2 + 3x) + (5x - 3x^2)$. -
Group like terms
Reorganize the expression to group like terms together:
$$(13x^2 - 3x^2) + (3x + 5x) - 2$$ -
Simplify the quadratic terms
Combine the $x^2$ terms:
$$13x^2 - 3x^2 = 10x^2$$ -
Simplify the linear terms
Combine the $x$ terms:
$$3x + 5x = 8x$$ -
Combine constant terms
Since the only constant term is $-2$, it remains:
The whole expression simplifies to:
$$10x^2 + 8x - 2$$
The simplified expression is $10x^2 + 8x - 2$.
More Information
The simplified result can be matched to one of the provided options. In this case, option C corresponds to the simplified expression.
Tips
- Not grouping like terms correctly: Make sure to arrange the expression by collecting similar terms (i.e., $x^2$ with $x^2$, $x$ with $x$, and constants with constants).
- Combining constants incorrectly: Always check that you are only combining like terms and not miscalculating the addition or subtraction.
AI-generated content may contain errors. Please verify critical information