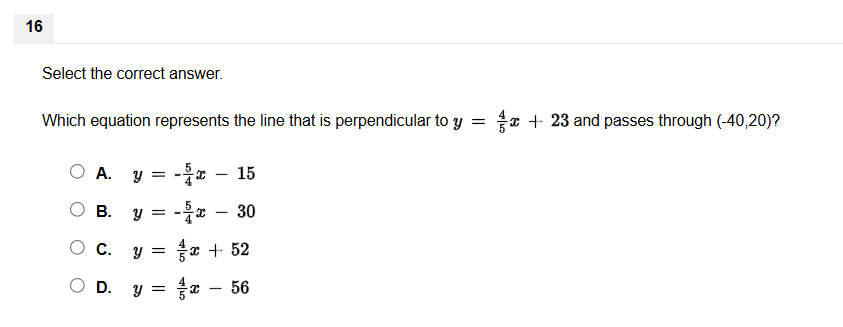
Which equation represents the line that is perpendicular to y = 4/5 x + 23 and passes through (-40, 20)?

Steps to Solve

1. Identify the slope of the given line The equation of the given line is in the slope-intercept form, $y = mx + b$. The slope ($m$) is $\frac{4}{5}$.

2. Determine the slope of the perpendicular line The slope of a line that is perpendicular to another is the negative reciprocal of the original slope. Therefore, the perpendicular slope is: $$ m_{\text{perpendicular}} = -\frac{1}{\frac{4}{5}} = -\frac{5}{4} $$

3. Use the point-slope form to find the equation The point-slope form of a line is given by: $$ y - y_1 = m(x - x_1) $$ where $(x_1, y_1)$ is the point the line passes through. Here, $(x_1, y_1) = (-40, 20)$ and $m = -\frac{5}{4}$.

Substituting these values into the equation: $$ y - 20 = -\frac{5}{4}(x + 40) $$

4. Simplify to slope-intercept form Distributing $-\frac{5}{4}$: $$ y - 20 = -\frac{5}{4}x - \frac{5}{4} \cdot 40 $$

Calculating $-\frac{5}{4} \cdot 40$: $$ -\frac{5}{4} \cdot 40 = -50 $$

Thus, the equation now is: $$ y - 20 = -\frac{5}{4}x - 50 $$

Now, add 20 to both sides: $$ y = -\frac{5}{4}x - 30 $$

5. Match with the provided options The equation can be compared with the options.

The equivalent form is: $$ y = -\frac{5}{4}x - 30 $$