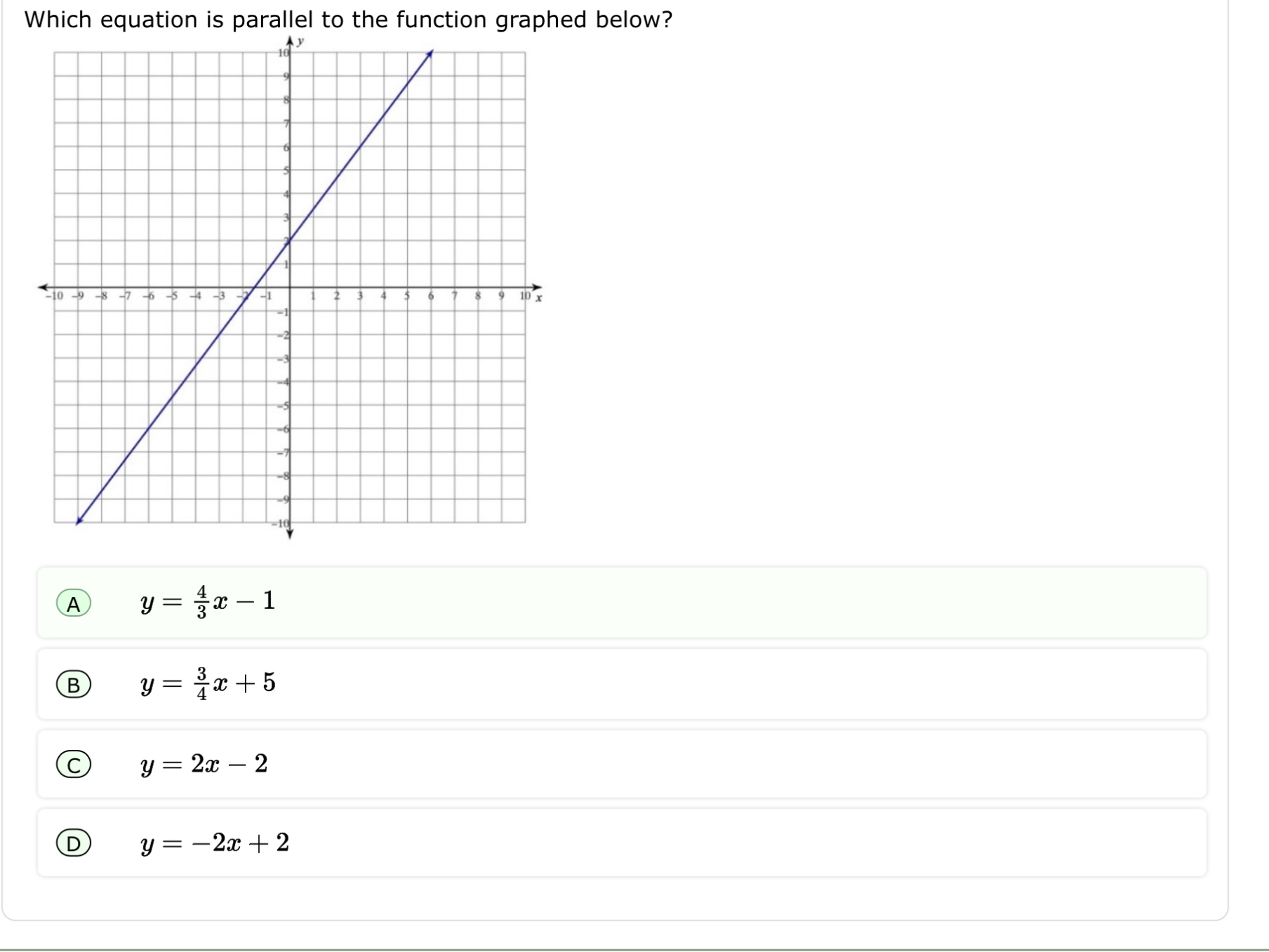
Which equation is parallel to the function graphed below?

Steps to Solve

1. Identify the slope of the line in the graph To determine the slope of the graphed line, select two clear points on the line. For example, if the line passes through the points (0, -1) and (3, 3), use the formula for slope:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Here, using (3, 3) and (0, -1): $$ m = \frac{3 - (-1)}{3 - 0} = \frac{4}{3} $$

So, the slope of the line in the graph is $\frac{4}{3}$.

2. Determine the slopes of the options provided Next, convert each equation to slope-intercept form ($y = mx + b$) to identify their slopes:

• For option A: $$ y = \frac{4}{3}x - 1 $$ Slope = $\frac{4}{3}$

• For option B: $$ y = \frac{3}{4}x + 5 $$ Slope = $\frac{3}{4}$

• For option C: $$ y = 2x - 2 $$ Slope = $2$

• For option D: $$ y = -2x + 2 $$ Slope = $-2$

3. Compare the slopes Lines that are parallel have the same slope. So, compare each option's slope to the slope of the graphed line $\frac{4}{3}$:

• Option A has slope $\frac{4}{3}$ (parallel).
• Option B has slope $\frac{3}{4}$ (not parallel).
• Option C has slope $2$ (not parallel).
• Option D has slope $-2$ (not parallel).

4. Select the parallel equation Choose the equation with the slope matching $\frac{4}{3}$, which is option A.