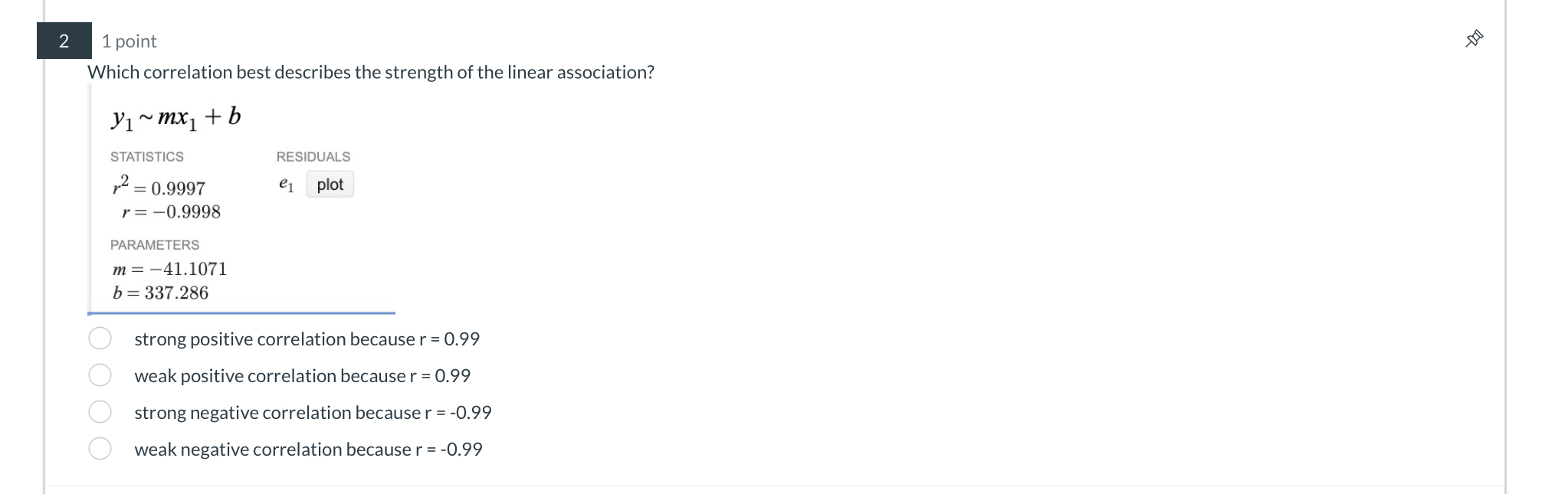
Which correlation best describes the strength of the linear association?
Understand the Problem
The question is asking to identify the type of correlation that best describes the strength of a linear association based on the provided statistics, specifically the correlation coefficient r and the coefficient of determination r².
Answer
strong negative correlation because \( r = -0.9998 \)
Answer for screen readers
The best description of the correlation is: strong negative correlation because ( r = -0.9998 ).
Steps to Solve
- Identify the correlation coefficient ( r )
The provided correlation coefficient ( r ) is ( -0.9998 ). This value is negative, indicating a negative correlation.
- Understand the strength of the correlation
The absolute value of ( r ) is ( |r| = 0.9998 ). Values of ( r ) close to 1 or -1 indicate a strong relationship.
- Determine the strength category
Typically:
- ( 0.70 \leq |r| < 1.00 ) indicates a strong correlation.
- ( 0.30 \leq |r| < 0.70 ) indicates a moderate correlation.
- ( |r| < 0.30 ) indicates a weak correlation.
Since ( |r| = 0.9998 ), this suggests a strong correlation.
- Decide on the type of correlation
Given that ( r ) is negative, this indicates that it is a strong negative correlation.
The best description of the correlation is: strong negative correlation because ( r = -0.9998 ).
More Information
The correlation coefficient ( r = -0.9998 ) indicates a very strong negative linear relationship between the two variables. This means that as one variable increases, the other decreases in a nearly perfect linear manner.
Tips
- Misinterpreting the sign of the correlation coefficient. Remember that a negative ( r ) indicates an inverse relationship.
- Confusing correlation strength with the direction of the relationship. High absolute values indicate strength, while the sign indicates the direction.
AI-generated content may contain errors. Please verify critical information