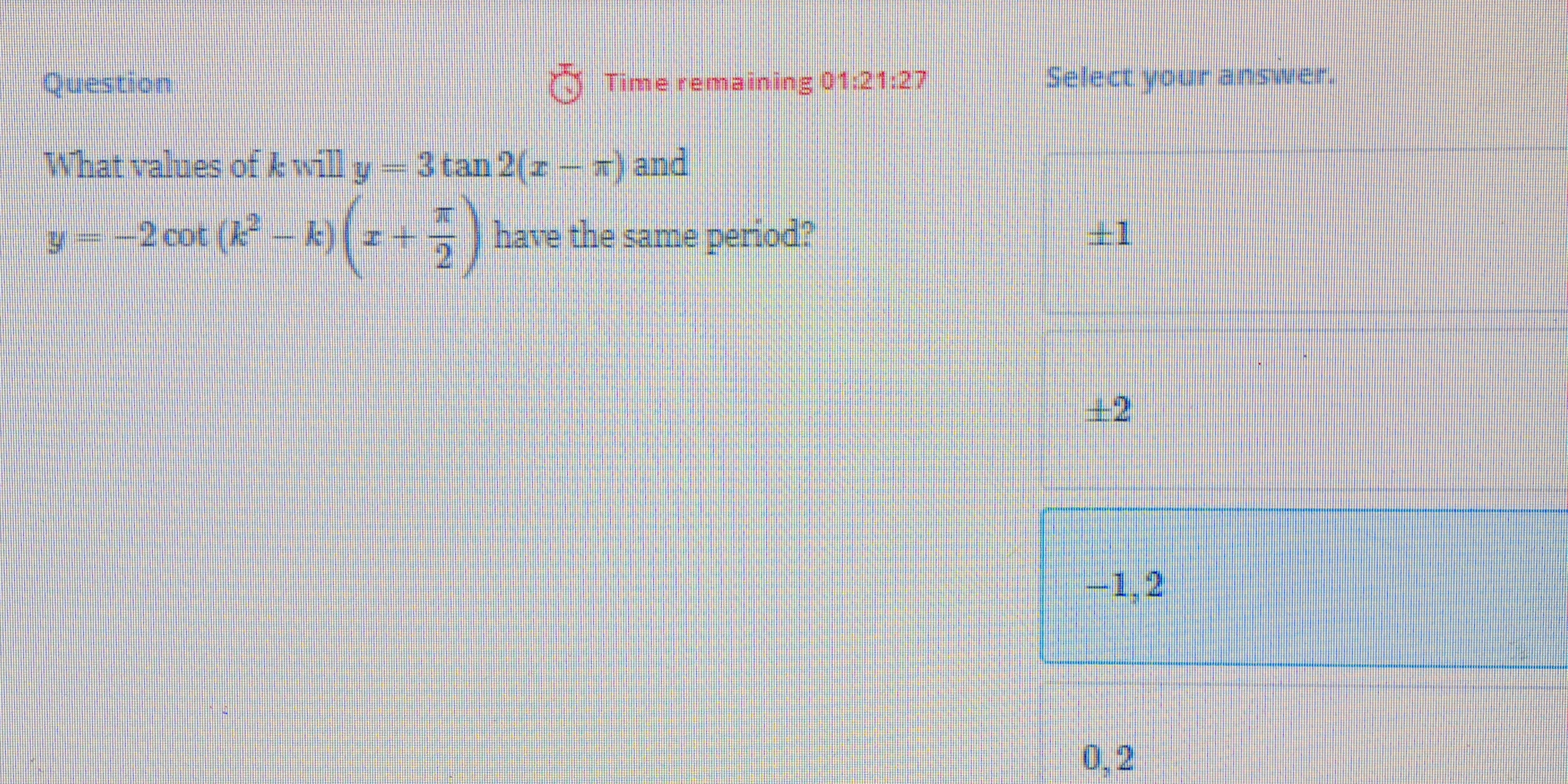
What values of k will y = 3 tan(2(x - π)) and y = -2 cot(k^2 - k)(x + π/2) have the same period?
Understand the Problem
The question is asking for the values of k that will make two given functions, which involve trigonometric functions, have the same period. This requires determining the periods of each function based on the parameters given and equating them.
Answer
The values of \( k \) are \( -1, 2 \).
Answer for screen readers
The values of ( k ) that will make the functions have the same period are ( k = -1 ) and ( k = 2 ).
Steps to Solve
- Identify the functions and their parameters
The first function is ( y = 3 \tan(2(x - \pi)) ) and the second function is ( y = -2 \cot((k^2 - k)(x + \frac{\pi}{2})) ).
- Determine the period of the first function
The period of ( \tan(bx) ) is given by ( \frac{\pi}{|b|} ).
In our case, ( b = 2 ):
$$ \text{Period of } y = 3 \tan(2(x - \pi)) = \frac{\pi}{2} $$
- Determine the period of the second function
The period of ( \cot(bx) ) is also given by ( \frac{\pi}{|b|} ).
Here, ( b = (k^2 - k) ):
$$ \text{Period of } y = -2 \cot((k^2 - k)(x + \frac{\pi}{2})) = \frac{\pi}{|k^2 - k|} $$
- Set the periods equal to each other
To find ( k ), we need the periods to be equal:
$$ \frac{\pi}{2} = \frac{\pi}{|k^2 - k|} $$
- Eliminate ( \pi ) and simplify
Dividing both sides by ( \pi ):
$$ \frac{1}{2} = \frac{1}{|k^2 - k|} $$
- Cross-multiply to solve for ( k )
Cross-multiplying gives:
$$ |k^2 - k| = 2 $$
This results in two equations:
Case 1:
$$ k^2 - k = 2 $$
Case 2:
$$ k^2 - k = -2 $$
- Solve the equations
For Case 1:
$$ k^2 - k - 2 = 0 $$
Factoring provides:
$$ (k - 2)(k + 1) = 0 $$
Solving gives:
$$ k = 2 \quad \text{or} \quad k = -1 $$
For Case 2:
$$ k^2 - k + 2 = 0 $$
Calculating the discriminant:
$$ \Delta = (-1)^2 - 4 \cdot 1 \cdot 2 = 1 - 8 = -7 $$
Since the discriminant is negative, there are no real solutions for this case.
- Final values of ( k )
Thus, the possible values for ( k ) from Case 1 are:
$$ k = 2 \quad \text{and} \quad k = -1 $$
The values of ( k ) that will make the functions have the same period are ( k = -1 ) and ( k = 2 ).
More Information
The functions are periodic and setting their periods equal allows for the identification of the values of ( k ) that satisfy the requirement. The ( \tan ) and ( \cot ) functions have standard periods that depend on their coefficients
Tips
- Neglecting to include the absolute value when equating the periods of the cotangent function.
- Miscalculating the discriminant when solving quadratic equations, which could lead to incorrect or imaginary solutions.
AI-generated content may contain errors. Please verify critical information