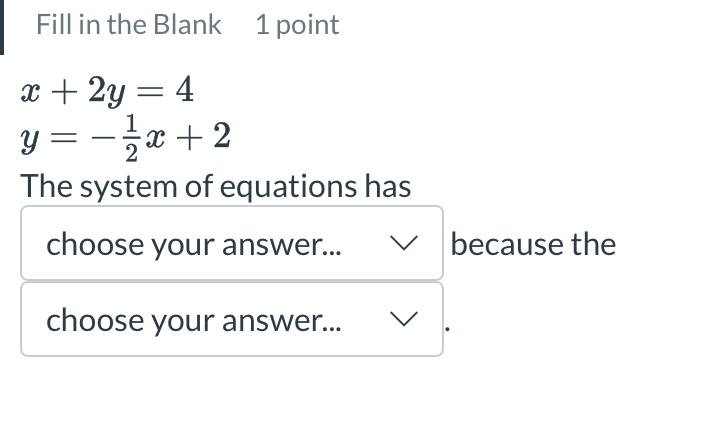
What type of system of equations is represented by the given equations?
Understand the Problem
The question is asking about the nature of a system of equations formed by the given two equations. It requires identification of whether the system has one solution, no solution, or infinitely many solutions based on their characteristics.
Answer
The system of equations has infinitely many solutions because the equations are identical.
Answer for screen readers
The system of equations has infinitely many solutions because the equations are identical.
Steps to Solve
- Convert the equations to slope-intercept form
We need to rewrite both equations in the form $y = mx + b$, where $m$ is the slope and $b$ is the y-intercept.
From the first equation: $$ x + 2y = 4 $$ Subtract $x$ from both sides: $$ 2y = -x + 4 $$ Now divide by 2: $$ y = -\frac{1}{2}x + 2 $$
The second equation is already in this form: $$ y = -\frac{1}{2}x + 2 $$
- Identify the slopes and intercepts
Both equations are now:
- $y = -\frac{1}{2}x + 2$ (first equation)
- $y = -\frac{1}{2}x + 2$ (second equation)
The slopes ($m$) are both $-\frac{1}{2}$, and the y-intercepts ($b$) are both $2$.
- Determine the nature of the system of equations
Since both equations have the same slope and the same y-intercept, this indicates they are identical lines.
- Conclusion about the system
A system of equations with identical lines has infinitely many solutions.
The system of equations has infinitely many solutions because the equations are identical.
More Information
When two equations represent the same line, every point on that line is a solution to both equations, leading to infinitely many solutions.
Tips
- Confusing parallel lines with identical lines: This system is not just parallel; they overlap completely.
- Not converting equations correctly to slope-intercept form can lead to misidentification of slopes and intercepts.
AI-generated content may contain errors. Please verify critical information