What number is equal to x if 10 + 2(3x + 1) = 72?
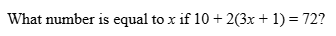
Understand the Problem
The question is asking us to find the value of x in the equation 10 + 2(3x + 1) = 72. To solve this, we will isolate x by performing algebraic manipulations.
Answer
The value of \( x \) is \( x = 10 \).
Answer for screen readers
The value of ( x ) is ( x = 10 ).
Steps to Solve
- Simplify the Equation We start with the original equation: $$ 10 + 2(3x + 1) = 72 $$
Distributing the 2 gives us: $$ 10 + 6x + 2 = 72 $$
-
Combine Like Terms Next, we combine the constants on the left side: $$ 12 + 6x = 72 $$
-
Isolate the Variable Subtract 12 from both sides of the equation: $$ 6x = 72 - 12 $$ $$ 6x = 60 $$
-
Solve for x Now, divide both sides by 6 to find x: $$ x = \frac{60}{6} $$ $$ x = 10 $$
The value of ( x ) is ( x = 10 ).
More Information
In this equation, we used the distributive property to simplify and isolate the variable ( x ). This process is common in algebra when solving linear equations.
Tips
- Forgetting to distribute: It's easy to miss distributing the number outside the parentheses. Always double-check that you apply the distributive property correctly.
- Combining constants incorrectly: Ensure that you correctly add or subtract constants. Double-check your arithmetic.
AI-generated content may contain errors. Please verify critical information