Find the length of the indicated side, to the nearest tenth of a metre.
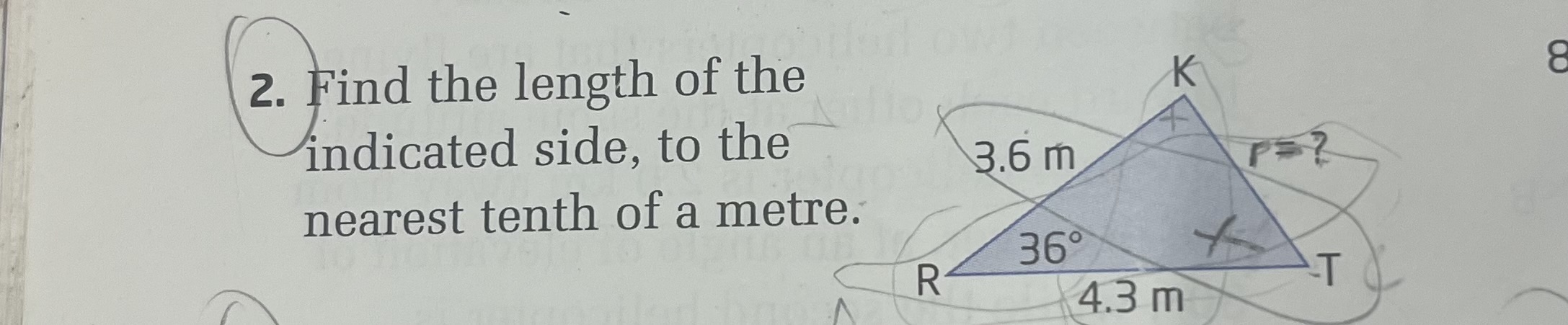
Understand the Problem
The question is asking us to find the length of a side of a triangle using trigonometric principles, specifically given one angle (36 degrees) and the lengths of the other two sides (3.6 m and 4.3 m). The solution requires applying the sine, cosine, or tangent functions to solve for the unknown side.
Answer
The length of the side \( KT \) is approximately \( 2.4 \, m \).
Answer for screen readers
The length of the indicated side ( KT ) is approximately ( 2.4 , m ).
Steps to Solve
- Identify the sides and the angle In triangle ( RKT ), we know:
- Side ( RK = 3.6 , m )
- Side ( RT = 4.3 , m )
- Angle ( R = 36^\circ )
We want to find the length of side ( KT ), denoted as ( x ).
- Use the Law of Cosines The Law of Cosines states: $$ c^2 = a^2 + b^2 - 2ab \cos(C) $$ Where ( C ) is the angle opposite side ( c ). In this case: $$ KT^2 = (RK)^2 + (RT)^2 - 2(RK)(RT) \cos(36^\circ) $$
Substituting the known values: $$ x^2 = (3.6)^2 + (4.3)^2 - 2(3.6)(4.3) \cos(36^\circ) $$
- Calculate the squares and cosine First, calculate the squares:
- ( (3.6)^2 = 12.96 )
- ( (4.3)^2 = 18.49 )
Now, find ( \cos(36^\circ) ): $$ \cos(36^\circ) \approx 0.8090 $$
Substituting these values into the equation: $$ x^2 = 12.96 + 18.49 - 2(3.6)(4.3)(0.8090) $$
- Perform the calculations Calculate ( 2(3.6)(4.3)(0.8090) ): $$ 2(3.6)(4.3)(0.8090) \approx 2(3.6)(4.3)(0.8090) \approx 25.579 $$
Now, substituting back in: $$ x^2 = 12.96 + 18.49 - 25.579 $$
-
Final calculation for ( x^2 ) Now perform the addition and subtraction: $$ x^2 \approx 31.45 - 25.579 $$ $$ x^2 \approx 5.871 $$
-
Find ( x ) Now, take the square root to find ( x ): $$ x \approx \sqrt{5.871} \approx 2.42 $$
Finally, round to the nearest tenth: $$ x \approx 2.4 , m $$
The length of the indicated side ( KT ) is approximately ( 2.4 , m ).
More Information
This triangle problem illustrates the application of the Law of Cosines, which is particularly useful in non-right triangles when two sides and the included angle are known.
Tips
- Misapplying the Law of Cosines: Ensure you identify the correct angle and corresponding opposite side.
- Not using the correct cosine value: Always use a calculator for precise trigonometric values.
- Squaring sides incorrectly: Double-check calculations for arithmetic errors.
AI-generated content may contain errors. Please verify critical information